Set Theory In Discrete Mathematics Owlcation We learn how to do formal proofs in set theory using intersections, unions, complements, and differences .more. Proof using set membership tables let a be a subset of a universal set u and let u ∈ u. to use this method we note that exactly one of the following is true: u ∈ a or u ∉ a. denote the situation where u ∈ a by 1 and that where u ∉ a by 0.

Introduction To Set Theory Discrete Mathematics Youtube Discrete This animated guide explains how to write proofs involving sets. techniques include proving subset, proving set equality, as well as incoporating powersets, unions, and intersections. link guide to set theory proofs. A first running example e going to see how to reason rigorously about sets and set theory. rather than doing t consider the following theorem: where a ⊆ b ∪ c, b ⊆ d, and c ⊆ e, we have a ⊆ d ∪ e. although there are a to of variables here, this result isn’t as scary as it might look. befor moving on, take a inute to think through. Prove: if n is odd, then n2 is odd. write a formal statement. ∀ integer k, ∃ integers m, n (2k 1) = m2 − n2. try out a few examples. find a pattern. every odd integer is equal to the difference between the squares of two integers. any odd integer can be written as (2k 1) for some integer k. we rewrite the expression as follows. Proof. suppose k 2 z and let k = fn 2 z : njkg and s = fn 2 z : njk2g. let x 2 k so that xjk. we can write k = ax for some a 2 z. then k2 = (ax)2 = x(a2x) so xjk2. thus, x 2 s. since any element x in k is also in s, we know that every element x in k is also in s, thus k s.
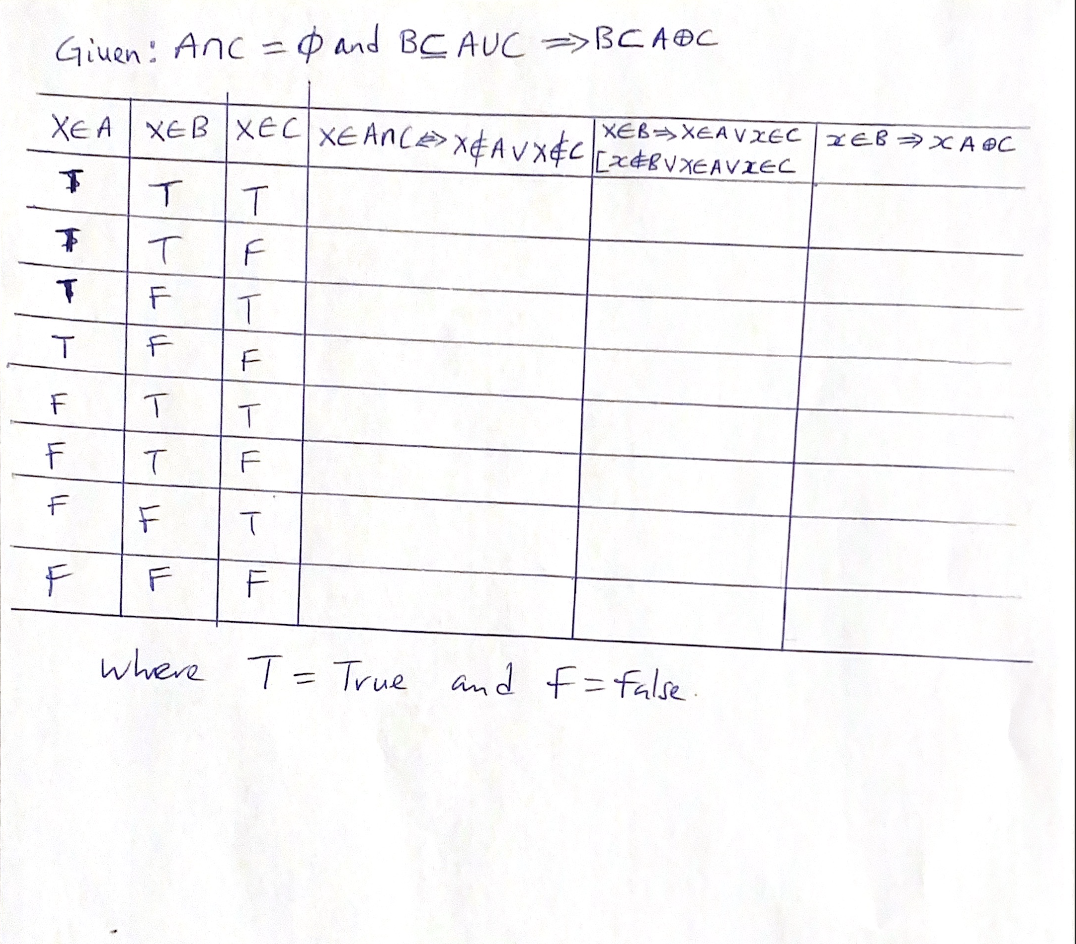
Solved Discrete Mathematics Logic Set Theory Proof A Chegg Prove: if n is odd, then n2 is odd. write a formal statement. ∀ integer k, ∃ integers m, n (2k 1) = m2 − n2. try out a few examples. find a pattern. every odd integer is equal to the difference between the squares of two integers. any odd integer can be written as (2k 1) for some integer k. we rewrite the expression as follows. Proof. suppose k 2 z and let k = fn 2 z : njkg and s = fn 2 z : njk2g. let x 2 k so that xjk. we can write k = ax for some a 2 z. then k2 = (ax)2 = x(a2x) so xjk2. thus, x 2 s. since any element x in k is also in s, we know that every element x in k is also in s, thus k s. The big tables, which explains what you can assume and what you can prove about different first order logic constructs; proof templates, which use the big tables to show how to structure proofs of definitions specified in first order logic; defining things, which explains how to define mathematical objects of different types; and. S 2 (1) prove that a b (2) prove that a is a proper subset of b. 1.2. operations on sets. let a and b be subsets of a set u. (1) the union of a and b, denoted a [ b, is the set of all elements that are in at least one of a or b. a [ b = fx 2 u j x 2 a or x 2 bg. Objectives on completing this course, students should be able to apply basic mathematical notation and arguments, including a variety of induction techniques. understand and be able to use the language of set theory; prove and disprove assertions using a variety of techniques. We learn how to do formal proofs in set theory using intersections, unions, complements, differences, and cartesian products (or cross products). more.

Solution Discrete Mathematics Set Theory Studypool The big tables, which explains what you can assume and what you can prove about different first order logic constructs; proof templates, which use the big tables to show how to structure proofs of definitions specified in first order logic; defining things, which explains how to define mathematical objects of different types; and. S 2 (1) prove that a b (2) prove that a is a proper subset of b. 1.2. operations on sets. let a and b be subsets of a set u. (1) the union of a and b, denoted a [ b, is the set of all elements that are in at least one of a or b. a [ b = fx 2 u j x 2 a or x 2 bg. Objectives on completing this course, students should be able to apply basic mathematical notation and arguments, including a variety of induction techniques. understand and be able to use the language of set theory; prove and disprove assertions using a variety of techniques. We learn how to do formal proofs in set theory using intersections, unions, complements, differences, and cartesian products (or cross products). more.

Set Theory Discrete Mathematics Study Notes Part 1 Know The Set Objectives on completing this course, students should be able to apply basic mathematical notation and arguments, including a variety of induction techniques. understand and be able to use the language of set theory; prove and disprove assertions using a variety of techniques. We learn how to do formal proofs in set theory using intersections, unions, complements, differences, and cartesian products (or cross products). more.

Set Theory Discrete Mathematics Study Notes Part 1 Know The Set
