How To Solve Exponential Equations Using Logarithms No Common Base Present

Solve Exponential Equations Using Logarithms Base 10 And Base E Learn how to solve exponential equations using logarithms when no common base is present. simple explanation by premath . Learn the techniques for solving exponential equations that requires the need of using logarithms, supported by detailed step by step examples. this is necessary because manipulating the exponential equation to establish a common base on both sides proves to be challenging.

Solve Exponential Equations Using Logarithms Base 2 And Other Bases We have used exponents to solve logarithmic equations and logarithms to solve exponential equations. we are now ready to combine our skills to solve equations that model real world situations, whether the unknown is in an exponent or in the argument of a logarithm. Demonstrates how to solve exponential equations by using logarithms. explains how to recognize when logarithms are necessary. provides worked examples showing how to obtain "exact" answers. In our first example we will use the laws of logs combined with factoring to solve an exponential equation whose terms do not have the same base. note how we rewrite the exponential terms as logarithms first. How to: given an exponential equation in which a common base cannot be found, solve for the unknown. apply the logarithm of both sides of the equation. if one of the terms in the equation has base 10, use the common logarithm. if none of the terms in the equation has base 10, use the natural logarithm.

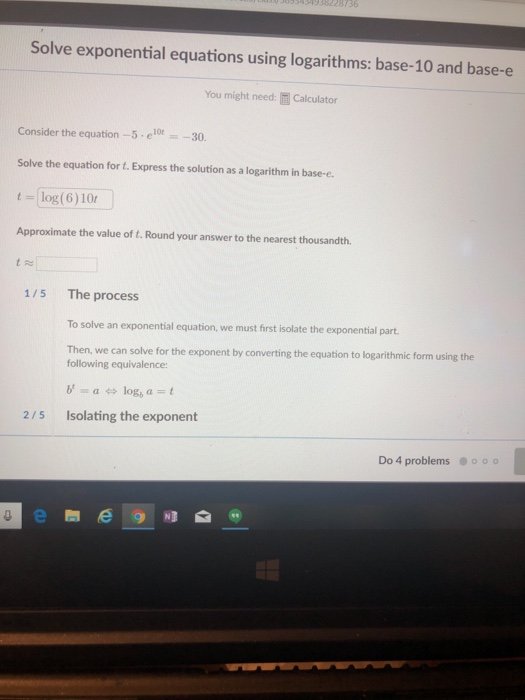
Solved Solve Exponential Equations Using Logarithms Base 10 Chegg In our first example we will use the laws of logs combined with factoring to solve an exponential equation whose terms do not have the same base. note how we rewrite the exponential terms as logarithms first. How to: given an exponential equation in which a common base cannot be found, solve for the unknown. apply the logarithm of both sides of the equation. if one of the terms in the equation has base 10, use the common logarithm. if none of the terms in the equation has base 10, use the natural logarithm. When the bases in an exponential equation cannot be made the same, taking the logarithm of each side is often the best way to solve it. for instance, in the equation 2 x = 3, there’s no simple way to express both sides with a common base, so logarithms are used instead. 18.4 first steps to solve exponential logarithmic equations to help you understand how to begin solving exponential and logarithmic equations, we give a guide to help you determine the rst step in nding a solution. This section covers solving exponential and logarithmic equations using algebraic techniques, properties of exponents and logarithms, and logarithmic conversions. Sometimes the common base for an exponential equation is not explicitly shown. in these cases, we simply rewrite the terms in the equation as powers with a common base, and solve using the one to one property. for example, consider the equation 256 = 4 x 5. we can rewrite both sides of this equation as a power of 2.