If A 1 1 2 1 B A 1 B 1 And A B 2 A 2 B 2 ⇒ a = 1 and b = 4. If the line 3y = 3x 1 is a normal to the ellipse (x^(2)) (5) (y^(2)) (b^(2))=1 then the length of the minor axis of the 5 b2 a ellipse is.
If A 1 1 2 1 B A 1 B 1 And A B 2 A 2 B 2 (a b)2 = a2 b2. equating the corresponding elements, we get. a = 1, b = 4 satisfy all four equations (i), (ii), (iii) and (iv). hence, a = 1, b = 4. if \ (a=\begin {bmatrix} 1 & 1 \\ [0.3em] 2 & 1 \\ [0.3em] \end {bmatrix}\) and \ (b=\begin {bmatrix} b)2 = a2 b2,then find the values of a and b . If a = b a b [1 2 1 2], b = [2 a 1 b] and if (a b) 2 = a 2 b 2 . find values of a and b. since (a b) 2 = a 2 b 2, (a b) (a b) = a 2 b 2. ∴ a 2 ab ba b 2 = a 2 b 2. ∴ ab ba = 0. ∴ ab = – ba. ∴ a b a b [1 2 1 2] [2 a 1 b] = [2 a 1 b] [1 2 1 2]. Given that, the three points are collinear. if the points (a1, b1), (a2, b2) and (a1 a2, b1 b2) are collinear, then (a) a1 b1=a2 b2 (b) a1 b2=a2 h1 (c) a a2=b1 b2 (d) a1 b2=a2 b1. check answer an. We have, a b=a 1 0b 2 −2 a2=1−12−11−12−1=−100−1b2=a1b−1a1b−1=a2 ba−1ab−bb 1 (a b)2=a 10b 2−2a 10b 2−2= (a 1)20 (a−1) (b 2)4∴ (a b)2=a2 b2⇒ (a 1)20 (a−1) (b 2)4=−100−1 a2 ba−1ab−bb 1⇒ (a 1)20 (a−1) (b 2)4=a2 b−1a−1ab−bb⇒a−1=0,b=4, (a 1)2=a2 b−1, (a−1) (b 2)=ab−b ⇒ a=1 and b=4.
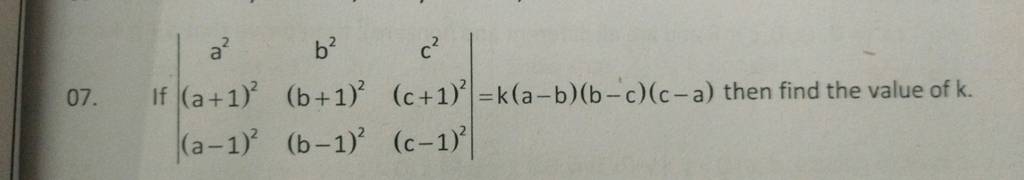
07 If в јв ј A2 A 1 2 Aв 1 2 B2 B 1 2 Bв 1 2 C2 C 1 2 Cв 1 2 в јв ј K Aв B Bв C Cв Given that, the three points are collinear. if the points (a1, b1), (a2, b2) and (a1 a2, b1 b2) are collinear, then (a) a1 b1=a2 b2 (b) a1 b2=a2 h1 (c) a a2=b1 b2 (d) a1 b2=a2 b1. check answer an. We have, a b=a 1 0b 2 −2 a2=1−12−11−12−1=−100−1b2=a1b−1a1b−1=a2 ba−1ab−bb 1 (a b)2=a 10b 2−2a 10b 2−2= (a 1)20 (a−1) (b 2)4∴ (a b)2=a2 b2⇒ (a 1)20 (a−1) (b 2)4=−100−1 a2 ba−1ab−bb 1⇒ (a 1)20 (a−1) (b 2)4=a2 b−1a−1ab−bb⇒a−1=0,b=4, (a 1)2=a2 b−1, (a−1) (b 2)=ab−b ⇒ a=1 and b=4. The correct answer is a=1 12 1,b=a 1b 1(a b)2=a2 b2⇒1 a−22 b−22=1−12−12 a−1b−12l.h.s1 a−22 b−21 a−22 b−2=a2 1 2a−4−2b−2−2a 42a 2 ab b−4−2b−2(2 b) 4=a2 2a−2b−3−2a 22a ab−b−2−2br.h.s=1−12−11−12−1 a−1b−1a−1b−1=−100−1 a2−b−a 1ab−b−b 1=a2−b−11−aab−b−bl.h.s=r.h.sa12. Thanks for watching this video lecture we are discussed some basic problem of complex number using demoivre's theorem ” .this video lecture helpful to polytechnic and engineering students. Find matrices a and b, where 2a – b = `[(1, 1),(0, 1)]` and a 3b = `[(1, 1),(0, 1)]` state whether the following statement is true or false: every square matrix of order n can be expressed as sum of symmetric and skew symmetric matrix. If three successive coefficients in the expansion of (x 2 x p ) n are in the ratio 21: 35: 40 and if the coefficient of the second term is 20 , then the values of n and p are respectively 10,2 8,4.
Find A 2 If A 0 1 3 B A 1 2 A B Numerade The correct answer is a=1 12 1,b=a 1b 1(a b)2=a2 b2⇒1 a−22 b−22=1−12−12 a−1b−12l.h.s1 a−22 b−21 a−22 b−2=a2 1 2a−4−2b−2−2a 42a 2 ab b−4−2b−2(2 b) 4=a2 2a−2b−3−2a 22a ab−b−2−2br.h.s=1−12−11−12−1 a−1b−1a−1b−1=−100−1 a2−b−a 1ab−b−b 1=a2−b−11−aab−b−bl.h.s=r.h.sa12. Thanks for watching this video lecture we are discussed some basic problem of complex number using demoivre's theorem ” .this video lecture helpful to polytechnic and engineering students. Find matrices a and b, where 2a – b = `[(1, 1),(0, 1)]` and a 3b = `[(1, 1),(0, 1)]` state whether the following statement is true or false: every square matrix of order n can be expressed as sum of symmetric and skew symmetric matrix. If three successive coefficients in the expansion of (x 2 x p ) n are in the ratio 21: 35: 40 and if the coefficient of the second term is 20 , then the values of n and p are respectively 10,2 8,4.

If A B 1 Then Prove That A 1 A 2 B 1 B 2 25 2 Where A Is Not Find matrices a and b, where 2a – b = `[(1, 1),(0, 1)]` and a 3b = `[(1, 1),(0, 1)]` state whether the following statement is true or false: every square matrix of order n can be expressed as sum of symmetric and skew symmetric matrix. If three successive coefficients in the expansion of (x 2 x p ) n are in the ratio 21: 35: 40 and if the coefficient of the second term is 20 , then the values of n and p are respectively 10,2 8,4.
