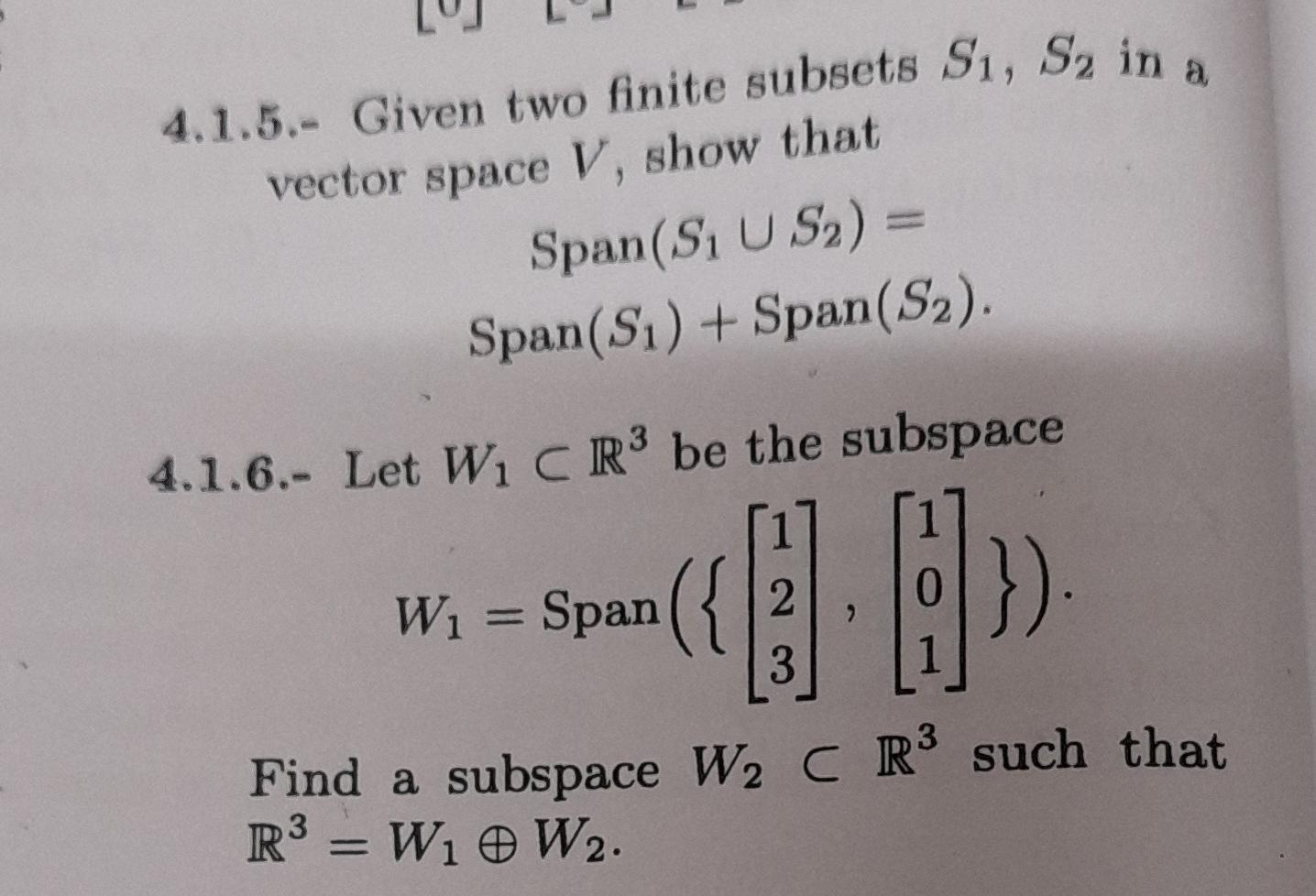
Solved 4 1 5 Given Two Finite Subsets S1 S2 In A Vector Chegg 1) since s, t are subspaces of v, the unique zero vector is contained in both, and so the zero vector is in the intersection. 2) let $a,b \in s \cap t$. that means a, b are in both, s and t. since $s,t$ are subspaces, they are closed under addition and so $a b$ is in s and in t and so in the intersection. 3) let c be an element of the reals. In this video we show that if s and t are finite subsets of a vector space and s is a subset of t then1) if s is linearly dependent, then so is t2) if t is l.

Solved 1 Let V Be Finite Dimensional Vector Space Let S T â L V I The zero vector is a linear combination of any nonempty set of vectors. the span of the empty set is the empty set. if s is a subset of a vector space v, then span (s) equals the intersection of all subspaces of v that contain s. in solving a system of linear equations, it is permissible to multiply an equation by any constant. Exercise 1.4.14: show that if s1 and s2 are arbitrary subsets of a vector space v , then span(s1 ∪ s2) = span(s1) span(s2). (the sum of two subsets is defined in the exercises in section 1.3). solution: in order to prove equality of two sets, we need to prove mutual inclu sion. ⊆: let v ∈ span(s1 ∪ s2). Fundamental theorem of linear algebra. suppose v is a vector space, s and t are finite subsets of v, s is independent and s ⊂ spant. then |s| ≤ |t|. remark. the proof should remind you of row reduction. proof. we induct on |t|. if |t| = 0 then t is the empty set, spant = {0} and s = ∅ since s is independent. thus |s| = 0 ≤ 0 = |t| in. Let s,t be subsets of a vector space v such that s⊆t. prove the following statements. (a) if s spans v, then so does t. (b) if t is linearly independent, so is s. problem 3. prove that if two vectors are linearly dependent, then one of them is a scalar multiple of the other. problem 4. let v be a vector space over f, and let {v1,v2,v3,v4} be a.

Solved Subspaces The Following Subsets Of The Vector Chegg Fundamental theorem of linear algebra. suppose v is a vector space, s and t are finite subsets of v, s is independent and s ⊂ spant. then |s| ≤ |t|. remark. the proof should remind you of row reduction. proof. we induct on |t|. if |t| = 0 then t is the empty set, spant = {0} and s = ∅ since s is independent. thus |s| = 0 ≤ 0 = |t| in. Let s,t be subsets of a vector space v such that s⊆t. prove the following statements. (a) if s spans v, then so does t. (b) if t is linearly independent, so is s. problem 3. prove that if two vectors are linearly dependent, then one of them is a scalar multiple of the other. problem 4. let v be a vector space over f, and let {v1,v2,v3,v4} be a. If w is a set of one or more vectors from a vector space v, then w is a subspace of v if and only if the following conditions hold. (a) if u and v are vectors in w, then u v is in w. There are two sets of tests to see if w is a subspace of v . the first set of tests is: note: a subspace is also closed under subtraction. theorem 1.1 (the intersection property). the intersection of subspaces of a vector space is itself a subspace. theorem 1.2 (intersection theorem). Let s0 and s be subsets of a vector space v. • s0 ⊂ s =⇒ span(s0) ⊂ span(s). • span(s0) = v and s0 ⊂ s =⇒ span(s) = v. • if v0,v1, ,vk is a spanning set for v and v0 is a linear combination of vectors v1, ,vk then v1, ,vk is also a spanning set for v. indeed, if v0 = r1v1 ··· rkvk, then. Given two subsets sand tof a vector space v, we construct two additional subsets of v; viz, s\t = fv2v jv2s and v2tg s[t = fv2v jv2s or v2tg when sand t are, in fact, subspaces of v, then natural questions to pose would be is s\t a subspace of v? and is s[t a subspace of v? these two questions were already posed in problems 4 amd 5 of homework.
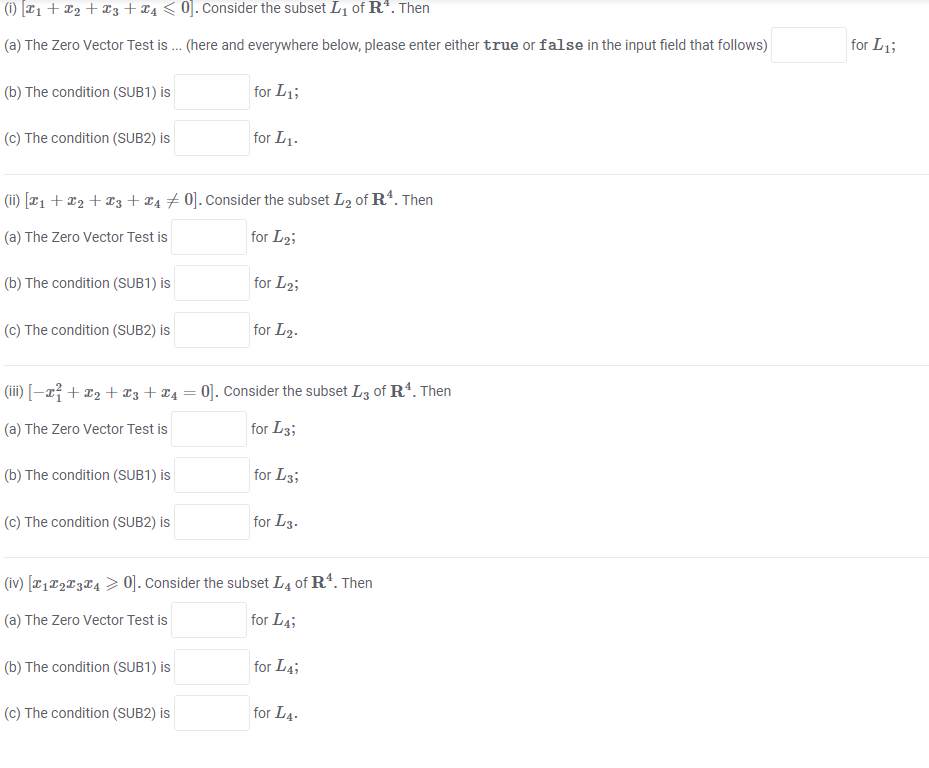
Solved Subspaces The Following Subsets Of The Vector Chegg If w is a set of one or more vectors from a vector space v, then w is a subspace of v if and only if the following conditions hold. (a) if u and v are vectors in w, then u v is in w. There are two sets of tests to see if w is a subspace of v . the first set of tests is: note: a subspace is also closed under subtraction. theorem 1.1 (the intersection property). the intersection of subspaces of a vector space is itself a subspace. theorem 1.2 (intersection theorem). Let s0 and s be subsets of a vector space v. • s0 ⊂ s =⇒ span(s0) ⊂ span(s). • span(s0) = v and s0 ⊂ s =⇒ span(s) = v. • if v0,v1, ,vk is a spanning set for v and v0 is a linear combination of vectors v1, ,vk then v1, ,vk is also a spanning set for v. indeed, if v0 = r1v1 ··· rkvk, then. Given two subsets sand tof a vector space v, we construct two additional subsets of v; viz, s\t = fv2v jv2s and v2tg s[t = fv2v jv2s or v2tg when sand t are, in fact, subspaces of v, then natural questions to pose would be is s\t a subspace of v? and is s[t a subspace of v? these two questions were already posed in problems 4 amd 5 of homework.
