If The Roots Of The Quadratic Equation C 2 Ab X 2 2 A 2 Bc X B 2 If the roots of the equation (c 2 – ab) x 2 – 2 (a 2 – bc) x b 2 – ac = 0 in x are equal, then show that either a = 0 or a 3 b 3 c 3 = 3abc. the given quadric equation is (c 2 a b) x 2 2 (a 2 b c) x (b 2 a c) = 0. then prove that either a = 0 or a 3 b 3 c 3 = 3 a b c. here. If the roots of the equation (c 2 − a b) x 2 − 2 (a 2 − b c) x (b 2 − a c) = 0 are real ane equal, show that either a = 0 o r (a 3 b 3 c 3) = 3 a b c.
If The Roots Of The Equation C 2 Ab X 2 2 A 2 Bc X B 2 Ac 0 Are Equal If the roots of the quadratic equation (c^2 ab)x^2 2(a^2 bc)x (b^2 ac) = 0 are equal, then the discriminant of the equation must be zero. the discriminant (d) of a quadratic equation ax^2 bx c = 0 is given by d = b^2 4ac . For the quadratic equation of the form (c² ab)x² 2(a² bc)x b² ac = 0, if the roots are equal, then the discriminant of the equation must be zero. the discriminant of a quadratic equation ax² bx c = 0 is given by Δ = b² 4ac. in this case, comparing to the general form, we have: a = c² ab; b = 2(a² bc) c = b² ac. If the roots of the equation (c^2 – ab)x^2 – 2(a^2 – bc)x b^2 – ac = 0 are real and equal prove that either a = 0 (or) a^3 b^3 c^3 = 3abc. If the roots of the equation (c2 ab) x2 2 (a2 bc) x b2 ac = 0 are equal, prove that either a = 0 or a3 b3 c3 = 3abc.
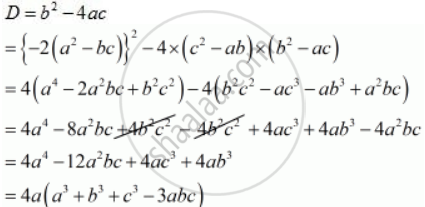
If The Roots Of The Equation C2 Ab X2 2 A2 Bc X B2 Ac 0 If the roots of the equation (c^2 – ab)x^2 – 2(a^2 – bc)x b^2 – ac = 0 are real and equal prove that either a = 0 (or) a^3 b^3 c^3 = 3abc. If the roots of the equation (c2 ab) x2 2 (a2 bc) x b2 ac = 0 are equal, prove that either a = 0 or a3 b3 c3 = 3abc. Ax² bx c = 0 , a = c² ab ; b = 2( a² bc ) ; c = b² ac ; it is given that , roots of the equation are equal , therefore , discriminant = 0 =>b² 4ac = 0 =>[ 2(a² bc)]² 4(c² ab ) (b² ac ) = 0 =>4(a⁴ 2a²bc b²c²) 4(b²c² ac³ ab³ a²bc)=0 =>4[a⁴ 2a² bc b²c² b² c² ac³ ab³ a²bc ]=0 =>a⁴ 3a²bc. If the roots of the equation (c2 – ab)x2 – 2(a2 – bc)x b2 – ac = 0 are real and equal prove that either a = 0 (or) a3 b3 c3 = 3abc. Roots of the equation. (c² ab)x² 2(a² bc)x (b² ac) = 0 are real and equal. as we know that, d = discriminant or b² 4ac. for real and equal roots : d = 0. by comparing this expression with general expression ax² bx c, we get. ⇒ a = (c² ab) and b = 2(a² bc) and c = (b² ac). ⇒ b² 4ac = 0. The roots of the equation 7x 2 x – 1 = 0 are: if the coefficient of x 2 and the constant term have the same sign and if the coefficient of x term is zero, then the quadratic equation has no real roots. find the value of ‘c’ for which the quadratic equation (c 1) x 2 6(c 1) x 3(c 9) = 0; c ≠ 1. has real and equal roots.
