If The Roots Of The Equation C 2 Ab X 2 2 A 2 Bc X B 2 Ac 0 Are Equal If the roots of the equation (c 2 – ab) x 2 – 2 (a 2 – bc) x b 2 – ac = 0 in x are equal, then show that either a = 0 or a 3 b 3 c 3 = 3abc. the given quadric equation is (c 2 a b) x 2 2 (a 2 b c) x (b 2 a c) = 0. then prove that either a = 0 or a 3 b 3 c 3 = 3 a b c. here. If the roots of the equation (c 2 – ab)x 2 – 2 (a 2 – bc)x b 2 – ac = 0 are real and equal prove that either a = 0 (or) a 3 b 3 c 3 = 3abc. (c 2 – ab)x 2 – 2 (a 2 – bc)x b 2 – ac = 0. here a = c 2 – ab; b = – 2 (a 2 – bc); c = b 2 – ac. since the roots are real and equal. ∆ = b 2 – 4ac. [– 2 (a 2 – bc)] 2 – 4 (c 2 – ab) (b 2 – ac) = 0.
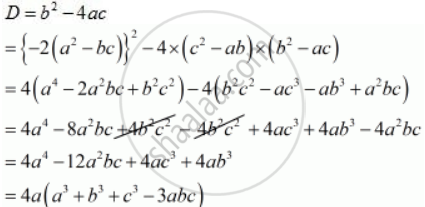
If The Roots Of The Equation C2 Ab X2 2 A2 Bc X B2 Ac 0 If the roots of the equation (c2 – ab) x2 2 (bc a2 ) x (b2 – ac) = 0 are equal , then prove that either a = 0 or a3 b3 c3 = 3abc. #math #quadraticequation. If the roots of the equation (c 2 ab)x 2 2 (a 2 bc)x b 2 ac=0 are equal, prove that either a=0 or a 3 b 3 c 3 =3abc. Given the equation (c 2 ab) x 2 2 (a 2 bc) x b 2 ac = 0. we need to see the nature of roots. roots of the quadratic equation are equal, then d=0. therefore if the roots of the equation (c 2 ab) x 2 2 (a 2 bc) x b 2 ac = 0 in x are equal, then a = 0 or a 3 b 3 c 3 = 3 abc. hence, the required option is 3. Explanation. roots of the equation. (c² ab)x² 2 (a² bc)x (b² ac) = 0 are real and equal. as we know that, d = discriminant or b² 4ac. for real and equal roots : d = 0. by comparing this expression with general expression ax² bx c, we get. ⇒ a = (c² ab) and b = 2 (a² bc) and c = (b² ac). ⇒ b² 4ac = 0.
6 If Roots Of Equation A2 B2 X2 2 Ac Bd X C2 D2 0 Has Equal Roots Pr Given the equation (c 2 ab) x 2 2 (a 2 bc) x b 2 ac = 0. we need to see the nature of roots. roots of the quadratic equation are equal, then d=0. therefore if the roots of the equation (c 2 ab) x 2 2 (a 2 bc) x b 2 ac = 0 in x are equal, then a = 0 or a 3 b 3 c 3 = 3 abc. hence, the required option is 3. Explanation. roots of the equation. (c² ab)x² 2 (a² bc)x (b² ac) = 0 are real and equal. as we know that, d = discriminant or b² 4ac. for real and equal roots : d = 0. by comparing this expression with general expression ax² bx c, we get. ⇒ a = (c² ab) and b = 2 (a² bc) and c = (b² ac). ⇒ b² 4ac = 0. The correct answer is given, (c2 ab)x2 2 (a2 bc)x b2 ac=0.if ax2 bx c=0 has equal roots then the discriminant b2 4ac=0.here a = c2 ab, b = 2 (a2 bc), c = b2 ac.⇒4 (a2 bc)2=4 ( 2a2 2bc) (b2 ac)⇒4a4 4b2c. If the roots of the quadratic equation (c^2 ab)x^2 2 (a^2 bc)x (b^2 ac) = 0 are equal, then the discriminant of the equation must be zero. the discriminant (d) of a quadratic equation ax^2 bx c = 0 is given by d = b^2 4ac. If the roots of the equation (c2 ab) x2 2 (a2 bc) x b2 ac = 0 are equal, prove that either a = 0 or a3 b3 c3 = 3abc. Putting the value of `a = (c^2 ab), b = 2 (a^2 bc) and c = (b^2 ac)` the given equation will have real roots, if d = 0. `4a (a^3 b^3 c^3 3abc) = 0` `a (a^3 b^3 c^3 3abc) = 0` so , either. a = 0. or. ` (a^3 b^3 c^3 3abc) = 0` `a^3 b^3 c^3 = 3abc` hence, a = 0 or `a^3 b^3 c^3 = 3abc`.
