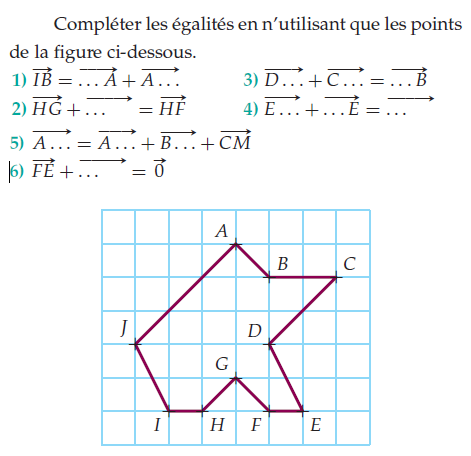
Imprimer Exercices Maths Seconde Vecteurs Dessin Bts Cpi Soient et deux vecteurs. calculer le produit scalaire −→u .−→v , puis déterminer une valeur approchée à 0,1 près de l’angle (−→u ; exercice 5 : produit scalaire norme et angle. exercice 6 : propriétés du produit scalaire. dans chaque cas suivants, les vecteurs et sont ils orthogonaux ? (le plan est muni d’un repère ortho normé). Exercice d'entrainement et leçon détaillée sur la notion de vecteurs pour les élèves de seconde au lycée. inclut des exercices corrigés au format pdf gratuits pour une meilleure compréhension.

Imprimer Exercice De Maths 2nde Dessin Bts Cpi Exercice 2 : abc est un triangle. 1. placer les points d, e et f tels que : ad = → 3 2 ab → 3 2 ac ; → be = → 1 2 cb → et f est le milieu de [ac]. 2. exprimer, en justifiant, le vecteur ab en fonction de → →fe. 3. a) exprimer le vecteur ae en fonction de → ab et → ac. →. Exercice 5 soient a et b deux points distants de 1,5 cm. 1) construire le point c tel que 5 2 bc ab. 2) construire le point d tel que 4 3 ad ab 3) démontrer la relation de colinéarité entre les vecteurs cd et ab. 4) en déduire la longueur du vecteur cd en cm. Représenter chacun de ces vecteurs. que constate t on ? associer à chaque égalité vectorielle la phrase correspondante et, dans chaque cas, illustrer par une figure. abcd est un parallélogramme. abdc est un parallélogramme. ia ib ?. Exprimer ⃗aa ' en fonction de ⃗ab et ⃗ac. c. démontrer que les points a, a’ et i sont alignés. 2. démontrer que le point g est le milieu de [ai]. 3. prouver que les droites (bc) et (ed) sont parallèles. 1. on considère le motif représenté ci dessous. l’image du point f par la translation de vecteur ⃗ba est.
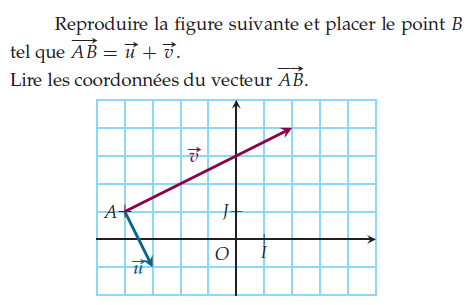
Vecteurs Exercices De Maths En 2de à Télécharger En Pdf Représenter chacun de ces vecteurs. que constate t on ? associer à chaque égalité vectorielle la phrase correspondante et, dans chaque cas, illustrer par une figure. abcd est un parallélogramme. abdc est un parallélogramme. ia ib ?. Exprimer ⃗aa ' en fonction de ⃗ab et ⃗ac. c. démontrer que les points a, a’ et i sont alignés. 2. démontrer que le point g est le milieu de [ai]. 3. prouver que les droites (bc) et (ed) sont parallèles. 1. on considère le motif représenté ci dessous. l’image du point f par la translation de vecteur ⃗ba est. Exercice 5 construire un repère (o; i, j) orthogonal. 1) placer les points a(3; 9) et b( 1; 5). 2) placer les points c et d tels que le quadrilatère abcd soit un parallélogramme de centre i. Exercice 1 nature d’un quadrilatère et droites remarquables on considère un repère orthonormé (o;i,j) du plan. on donne les points a( 1;6),b(7; 2),c(1; 2) et. Déterminer un vecteur unitaire orthogonal aux vecteurs ⃗u (3; 1; −2) et ⃗v (2; 1; 4) exercices sur le calcul vectoriel – auteur pierre lux. Exprimer les vecteurs −−→ bc et −−→ bd en fonction des seuls vecteurs −−→ ab et −→ ac signifie que l’on veut des égalités du type : −−→ bc = x −−→ ab y −→ ac et −−→ bd = x′ −−→ ab y′ −→ ac en fonction de 3. on remarque que −−→ bd = −2 −−→ bc. les vecteurs −−.

Vecteurs Cours Pdf à Imprimer Maths Seconde Exercice 5 construire un repère (o; i, j) orthogonal. 1) placer les points a(3; 9) et b( 1; 5). 2) placer les points c et d tels que le quadrilatère abcd soit un parallélogramme de centre i. Exercice 1 nature d’un quadrilatère et droites remarquables on considère un repère orthonormé (o;i,j) du plan. on donne les points a( 1;6),b(7; 2),c(1; 2) et. Déterminer un vecteur unitaire orthogonal aux vecteurs ⃗u (3; 1; −2) et ⃗v (2; 1; 4) exercices sur le calcul vectoriel – auteur pierre lux. Exprimer les vecteurs −−→ bc et −−→ bd en fonction des seuls vecteurs −−→ ab et −→ ac signifie que l’on veut des égalités du type : −−→ bc = x −−→ ab y −→ ac et −−→ bd = x′ −−→ ab y′ −→ ac en fonction de 3. on remarque que −−→ bd = −2 −−→ bc. les vecteurs −−.

Devoir Maison Seconde Maths Vecteurs Ventana Blog Déterminer un vecteur unitaire orthogonal aux vecteurs ⃗u (3; 1; −2) et ⃗v (2; 1; 4) exercices sur le calcul vectoriel – auteur pierre lux. Exprimer les vecteurs −−→ bc et −−→ bd en fonction des seuls vecteurs −−→ ab et −→ ac signifie que l’on veut des égalités du type : −−→ bc = x −−→ ab y −→ ac et −−→ bd = x′ −−→ ab y′ −→ ac en fonction de 3. on remarque que −−→ bd = −2 −−→ bc. les vecteurs −−.

Exercices De Maths Seconde Avec Corriges Pdf Communautテゥ Mcms邃
