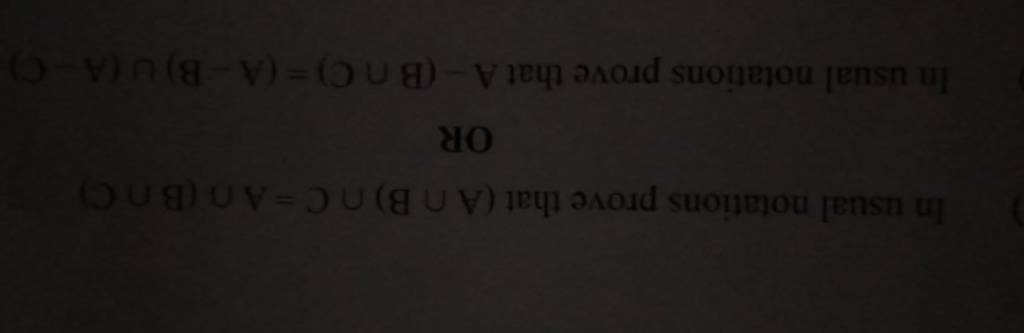
In Usual Notations Prove That Aв B в C Aв Bв C Or In Usual Notations Prove Using the pythagorean theorem in abd and adc, we get: ad2 bd2 =ab2 ⇒h2 x2 =c2 ad2 dc 2 =ac 2 ⇒ h2 (b−x)2 = a2. equating the two expressions for h2, we get: c2 −x2 =a2 −(b−x)2 expanding and simplifying, we get: c2 −x2 =a2 −b2 2bx−x2 c2 =a2 −b2 2bx since x = bcosa, we substitute x to get: c2 =a2 −b2 2b(bcosa) a2 = b2 c2 −2bccosa. In any Δabc, with usual notations, prove that b 2 = c 2 a 2 – 2ca cos b. i.e. b as origin, x axis along the line bc and the y axis perpendicular to the line bc. in the two figures, ∠b is shown as acute in one and obtuse in the other. solutions of triangle. is there an error in this question or solution?.

In Triangle Abc With Usual Notations Prove That A B 2cos 2 C2 12th std maths example 6.1 with usual notation in any triangle prove that a2=b2 c2 2bccosa, b2=c2 a2. Recognize that cos2a sin2a=1, so b^ {2}\cos^ {2}a b^ {2}\sin^ {2}a = b^ {2} b2cos2a b2sin2a=b2 combine like terms to get c^ {2} b^ {2} 2bc\cos a = bc^ {2} c2 b2−2bccosa=bc2. Sajal and kajal are partners sharing profits and losses in the ratio of 21. on 1st april, 2021, their coced were: sajal ₹ 5,00,000 and kajal ₹ 4,00,000. prepare profit \& loss appropriation account and the partners' capital accounts at the end of the yea lisa the following information:. 1 mathematics b i [ vectors & mechanics (i)], 4 cr. hours, for students of b.s.mathematics (combination i & ii) 2 mathematics b course i: vector and mechanic.

In Triangle Abc With Usual Notations Prove That A B 2cos 2 C2 Sajal and kajal are partners sharing profits and losses in the ratio of 21. on 1st april, 2021, their coced were: sajal ₹ 5,00,000 and kajal ₹ 4,00,000. prepare profit \& loss appropriation account and the partners' capital accounts at the end of the yea lisa the following information:. 1 mathematics b i [ vectors & mechanics (i)], 4 cr. hours, for students of b.s.mathematics (combination i & ii) 2 mathematics b course i: vector and mechanic. Example 8 (i):prove that in any triangle abc a2=b2 c2 2bc cos a. proof of cosine law using vectors. To prove the law of cosines, we will use the triangle and the cosine definition. for the quadratic equation, we will complete the square to show the conic section it represents. in triangle abc, apply the law of cosines: a^2 = b^2 c^2 2bc cos a. to derive this, consider the coordinates of points a, b, and c in the cartesian plane. We proved that for triangle abc with altitude cd, the relationship a2 = b2 c2 − 2bccosa holds true by applying the pythagorean theorem and cosine ratio in right triangles acd and bcd. Given, abc is a triangle. to find, prove that a²=b² c² 2bc cos a. solution, Δabc is a triangle. in this a vector b vector c vector=0 ⇒b vector c vector= a vector then, squaring both the sides, ⇒ (b vector c vector)²= ( a vector)² ⇒ (b vector c vector) (b vector c vector)= ( a vector) ( a vector).

In Any Triangle δ Abc With Usual Notations Prove That B 2 C 2 A Example 8 (i):prove that in any triangle abc a2=b2 c2 2bc cos a. proof of cosine law using vectors. To prove the law of cosines, we will use the triangle and the cosine definition. for the quadratic equation, we will complete the square to show the conic section it represents. in triangle abc, apply the law of cosines: a^2 = b^2 c^2 2bc cos a. to derive this, consider the coordinates of points a, b, and c in the cartesian plane. We proved that for triangle abc with altitude cd, the relationship a2 = b2 c2 − 2bccosa holds true by applying the pythagorean theorem and cosine ratio in right triangles acd and bcd. Given, abc is a triangle. to find, prove that a²=b² c² 2bc cos a. solution, Δabc is a triangle. in this a vector b vector c vector=0 ⇒b vector c vector= a vector then, squaring both the sides, ⇒ (b vector c vector)²= ( a vector)² ⇒ (b vector c vector) (b vector c vector)= ( a vector) ( a vector).

In Any δabc With Usual Notations Prove That B2 C2 A2 2ca Cosb We proved that for triangle abc with altitude cd, the relationship a2 = b2 c2 − 2bccosa holds true by applying the pythagorean theorem and cosine ratio in right triangles acd and bcd. Given, abc is a triangle. to find, prove that a²=b² c² 2bc cos a. solution, Δabc is a triangle. in this a vector b vector c vector=0 ⇒b vector c vector= a vector then, squaring both the sides, ⇒ (b vector c vector)²= ( a vector)² ⇒ (b vector c vector) (b vector c vector)= ( a vector) ( a vector).

In δ Abc With Usual Notations Prove That A B 2 Cos 2 C2 A
