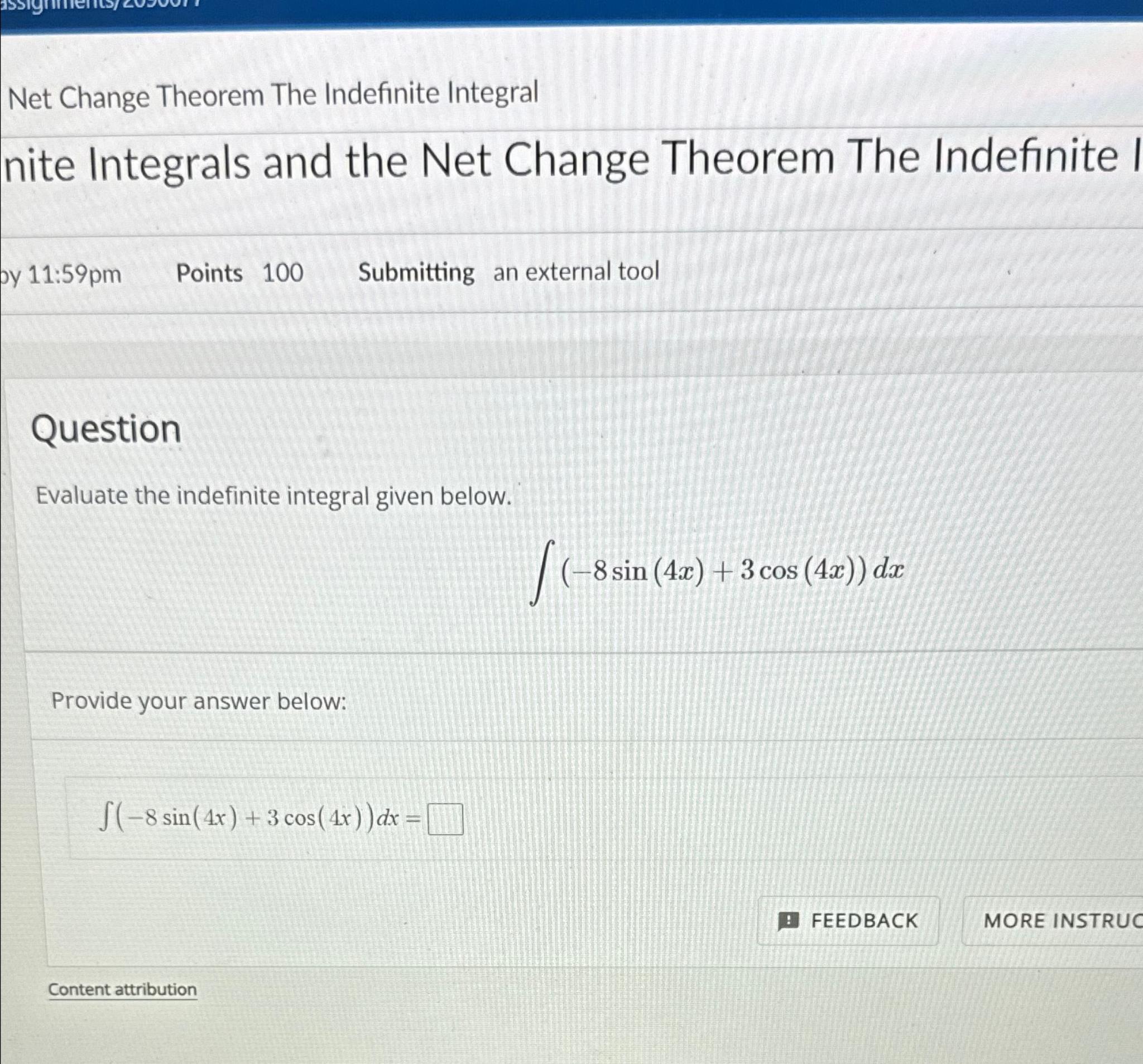
Solved Net Change Theorem The Indefinite Integralnite Chegg @themathsorcerer walks us through the concept of the net change theorem, which states that the net change in a function is the definite integral of its deriv. 5.4 indefinite integrals and the net change theorem the fundamental theorem of calculus tells us that an anti derivative of a continuous function f de fined on an interval cointaining a may be written f(x) = rx a f(t)dt. given this relationship between anti derivatives and integrals we introduce a new notation for anti derivatives: f(x) = z.

Indefinite Integrals And The Net Change Theorem Pdf Integral Velocity Explain the significance of the net change theorem. use the net change theorem to solve applied problems. apply the integrals of odd and even functions. The net change theorem considers the integral of a rate of change. it says that when a quantity changes, the new value equals the initial value plus the integral of the rate of change of that quantity. Net change theorem. part 2 of the fundamental theorem says that if f is continuous on [a,b], then zb a f(x)dx = f(b)−f(a) where f is any antiderivative of f. this means that f′ = f, so the equation can be rewritten as zb a f′(x)dx = f(b) −f(a). This says that the definite integral of the rate of change of a quantity gives the net change in the quantity. the text calls this fact the net change theorem. for \(f(t)\) a velocity, displacement is net change.
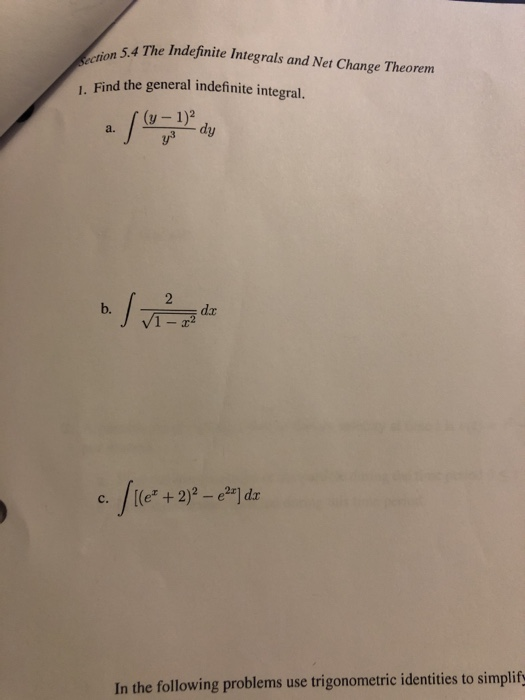
Solved 5 4 The Indefinite Integrals And Net Change Theorem Chegg Net change theorem. part 2 of the fundamental theorem says that if f is continuous on [a,b], then zb a f(x)dx = f(b)−f(a) where f is any antiderivative of f. this means that f′ = f, so the equation can be rewritten as zb a f′(x)dx = f(b) −f(a). This says that the definite integral of the rate of change of a quantity gives the net change in the quantity. the text calls this fact the net change theorem. for \(f(t)\) a velocity, displacement is net change. 4.4 inde nite integrals and the net change theorem an integral without limits of integration attached, z f(x)dx, is called an inde nite integral and is used to represent any antiderivative of f(x), that is, z f(x)dx= f(x) cwhere f0(x) = f(x). examples: 1. z x 2 dx= x 1 c, d dx ( x 1 c) = x 2 2. z sec2(x)dx= tan(x) c, d dx (tan(x) c) = sec2(x. The net change theorem, which is a restatement of the ftc ii from a different perspective, says that the net change in a function is the definite integral of its derivative. $$\int a^b f'(x)\, dx = f(b) f(a)$$. Note: indefinite integrals are those integrals without boundary, i.e. ∫f (x)dx. ∫f (x)dx =f(x) c; where . f'(x) = f (x) ex: evaluate the following integrals: a) ∫(5x−1)(x 3)dx. It defines indefinite integrals as representing an entire family of antiderivatives rather than a single function. the net change theorem states that the integral of a rate of change between two values is equal to the net change in the related function over that interval.

5 4 Indefinite Integrals And The Net Change Theorem 1 Definition 4.4 inde nite integrals and the net change theorem an integral without limits of integration attached, z f(x)dx, is called an inde nite integral and is used to represent any antiderivative of f(x), that is, z f(x)dx= f(x) cwhere f0(x) = f(x). examples: 1. z x 2 dx= x 1 c, d dx ( x 1 c) = x 2 2. z sec2(x)dx= tan(x) c, d dx (tan(x) c) = sec2(x. The net change theorem, which is a restatement of the ftc ii from a different perspective, says that the net change in a function is the definite integral of its derivative. $$\int a^b f'(x)\, dx = f(b) f(a)$$. Note: indefinite integrals are those integrals without boundary, i.e. ∫f (x)dx. ∫f (x)dx =f(x) c; where . f'(x) = f (x) ex: evaluate the following integrals: a) ∫(5x−1)(x 3)dx. It defines indefinite integrals as representing an entire family of antiderivatives rather than a single function. the net change theorem states that the integral of a rate of change between two values is equal to the net change in the related function over that interval.
