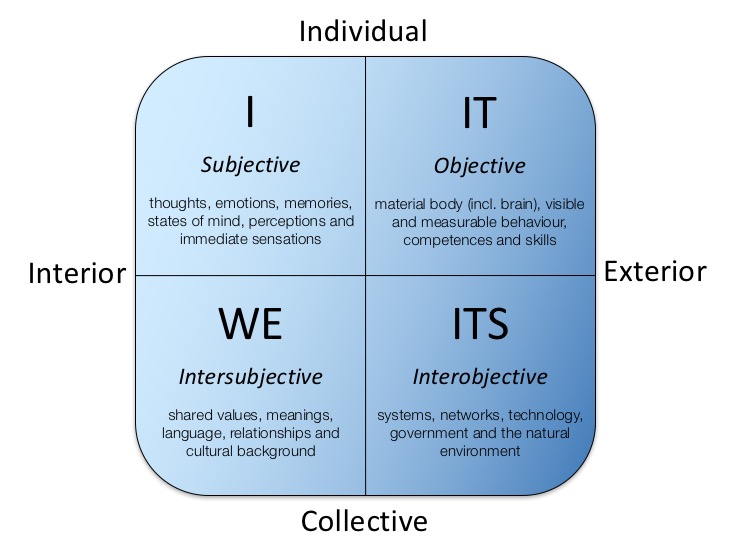
Integral Theory %d1%82%d0%bb%d0%b5 Spiral Dynamics Integral

An Introduction To Spiral Dynamics Integral A Holistic Framework For The integral which you describe has no closed form which is to say that it cannot be expressed in elementary functions. for example, you can express $\int x^2 \mathrm {d}x$ in elementary functions such as $\frac {x^3} {3} c$. Answers to the question of the integral of $\frac {1} {x}$ are all based on an implicit assumption that the upper and lower limits of the integral are both positive real numbers.

Integral Theory тле Spiral Dynamics Integral The improper integral $\int a^\infty f (x) \, dx$ is called convergent if the corresponding limit exists and divergent if the limit does not exist. while i can understand this intuitively, i have an issue with saying that the mathematical object we defined as improper integrals is "convergent" or "divergent". You will get the same answer because when you perform a change of variables, you change the limits of your integral as well (integrating in the complex plane requires defining a contour, of course, so you'll have to be careful about this). The integral of 0 is c, because the derivative of c is zero. also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f (x)=c will have a slope of zero at point on the function. Then your original integral goes from: $$ \int e^ {f (x)}dx $$ to $$ \int \frac {e^u} {f' (x)}du. $$ of course, this is not always so easy to integrate, as moron points out.
Integral Theory тле Spiral Dynamics Integral The integral of 0 is c, because the derivative of c is zero. also, it makes sense logically if you recall the fact that the derivative of the function is the function's slope, because any function f (x)=c will have a slope of zero at point on the function. Then your original integral goes from: $$ \int e^ {f (x)}dx $$ to $$ \int \frac {e^u} {f' (x)}du. $$ of course, this is not always so easy to integrate, as moron points out. I've been learning the fundamental theorem of calculus. so, i can intuitively grasp that the derivative of the integral of a given function brings you back to that function. is this also the case. If by integral you mean the cumulative distribution function $\phi (x)$ mentioned in the comments by the op, then your assertion is incorrect. This question is just idle curiosity. today i find that an integral problem can be easily evaluated by using simple techniques like my answer to evaluate \begin {equation} \int 0^ {\pi 2}\frac {\cos {. I was reading on in this article about the n dimensional and functional generalization of the gaussian integral. in particular, i would like to understand how the following equations are.

Spiral Dynamics Integral I've been learning the fundamental theorem of calculus. so, i can intuitively grasp that the derivative of the integral of a given function brings you back to that function. is this also the case. If by integral you mean the cumulative distribution function $\phi (x)$ mentioned in the comments by the op, then your assertion is incorrect. This question is just idle curiosity. today i find that an integral problem can be easily evaluated by using simple techniques like my answer to evaluate \begin {equation} \int 0^ {\pi 2}\frac {\cos {. I was reading on in this article about the n dimensional and functional generalization of the gaussian integral. in particular, i would like to understand how the following equations are.

Integral Theory тле Spiral Dynamics Integral This question is just idle curiosity. today i find that an integral problem can be easily evaluated by using simple techniques like my answer to evaluate \begin {equation} \int 0^ {\pi 2}\frac {\cos {. I was reading on in this article about the n dimensional and functional generalization of the gaussian integral. in particular, i would like to understand how the following equations are.
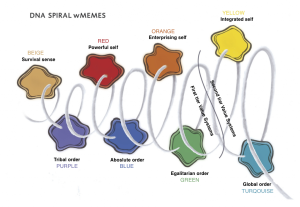
Theory Value Systems тле Spiral Dynamics Integral
Comments are closed.