
Irrational Numbers Definition Common Examples Diagram 55 Off Irrational numbers are numbers that are neither terminating nor recurring and cannot be expressed as a ratio of integers. get the properties, examples, symbol and the list of irrational numbers at byju's. Irrational numbers are real numbers that cannot be written as a simple fraction or ratio. in simple words, the irrational numbers are those numbers those are not rational. hippasus, a greek philosopher and a pythagorean, discovered the first evidence of irrational numbers 5th century bc.
Irrational Numbers Definition Common Examples Diagram 60 Off Irrational means not rational (no ratio) let's look at what makes a number rational or irrational a rational number can be written as a ratio of two integers (ie a simple fraction). example: 1.5 is rational, because it can be written as the ratio 3 2. example: 7 is rational, because it can be written as the ratio 7 1. An irrational number is a real number that you can’t write as a simple fraction. it has a decimal that goes on forever without repeating. examples include √2 and π. are irrational numbers real numbers? yes, all irrational numbers are real numbers. what are five examples of irrational numbers? some examples are: √2, π, e, φ, and √11. Common examples of irrational numbers are: while discussing rational and irrational numbers, we need to compare them to find how terms mathematically differ from each other. below are the differences between rational and irrational numbers in a table. include perfect squares such as 1, 4, 9, 16, 25, 36. Irrational numbers are the set of real numbers that cannot be expressed in the form of a fraction, p q where p and q are integers. the denominator q is not equal to zero (q ≠ 0). also, the decimal expansion of an irrational number is neither terminating nor repeating.
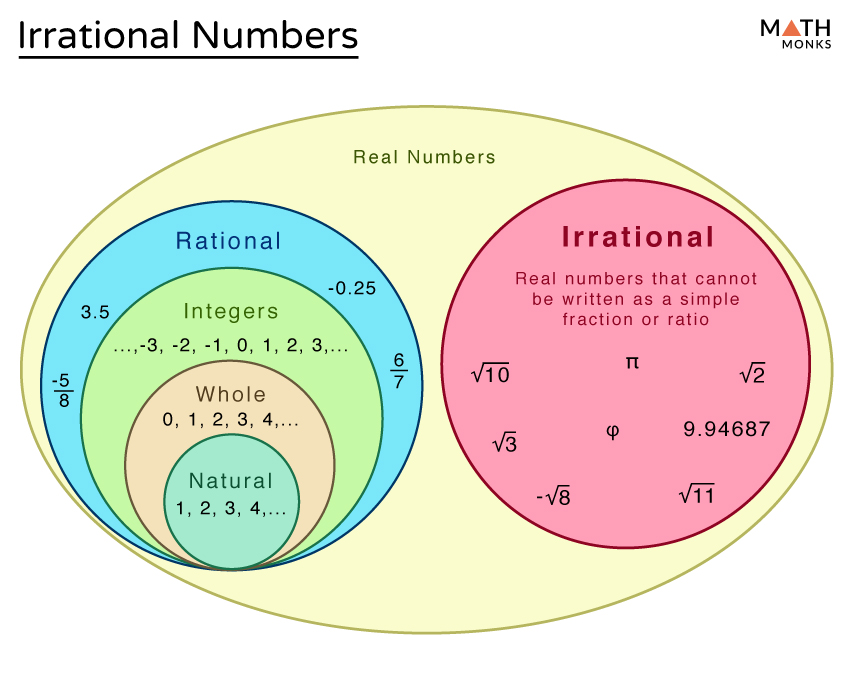
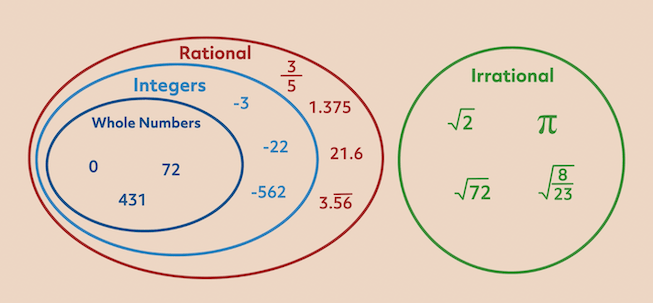
Irrational Numbers Definition Common Examples Diagram 60 Off Common examples of irrational numbers are: while discussing rational and irrational numbers, we need to compare them to find how terms mathematically differ from each other. below are the differences between rational and irrational numbers in a table. include perfect squares such as 1, 4, 9, 16, 25, 36. Irrational numbers are the set of real numbers that cannot be expressed in the form of a fraction, p q where p and q are integers. the denominator q is not equal to zero (q ≠ 0). also, the decimal expansion of an irrational number is neither terminating nor repeating. Examples of irrational numbers: √2, √3, π, e, – √ 7, etc. in this article, we will learn about irrational numbers, their properties, examples, identification, and others in detail. we will also discuss numerical examples and worksheet on irrational numbers. Irrational numbers are the type of real numbers that cannot be expressed in the form p q, q ≠ 0. these numbers include non terminating, non repeating decimals. rational and irrational numbers together make real numbers. An irrational number is a number that cannot be expressed as the ratio of two integers. its decimal representation is infinite and non repeating, meaning the digits after the decimal point continue endlessly without forming a regular pattern. The venn diagram below shows examples of all the different types of rational, irrational numbers including integers, whole numbers, repeating decimals and more. you can express 5 as 5 1 5 1 which is the quotient of the integer 5 and 1. you can express 2 as 2 1 2 1 which is the quotient of the integer 2 and 1.

Irrational Numbers Pdf Examples of irrational numbers: √2, √3, π, e, – √ 7, etc. in this article, we will learn about irrational numbers, their properties, examples, identification, and others in detail. we will also discuss numerical examples and worksheet on irrational numbers. Irrational numbers are the type of real numbers that cannot be expressed in the form p q, q ≠ 0. these numbers include non terminating, non repeating decimals. rational and irrational numbers together make real numbers. An irrational number is a number that cannot be expressed as the ratio of two integers. its decimal representation is infinite and non repeating, meaning the digits after the decimal point continue endlessly without forming a regular pattern. The venn diagram below shows examples of all the different types of rational, irrational numbers including integers, whole numbers, repeating decimals and more. you can express 5 as 5 1 5 1 which is the quotient of the integer 5 and 1. you can express 2 as 2 1 2 1 which is the quotient of the integer 2 and 1.

Irrational Numbers Examples Format Pdf An irrational number is a number that cannot be expressed as the ratio of two integers. its decimal representation is infinite and non repeating, meaning the digits after the decimal point continue endlessly without forming a regular pattern. The venn diagram below shows examples of all the different types of rational, irrational numbers including integers, whole numbers, repeating decimals and more. you can express 5 as 5 1 5 1 which is the quotient of the integer 5 and 1. you can express 2 as 2 1 2 1 which is the quotient of the integer 2 and 1.

Irrational Numbers Examples Format Pdf
