
Lambert W Function Pdf Used to solve equations in which the unknown appears both outside and inside an exponential function or a logarithm. This page was last modified 12:36, 26 april 2007. cz is free.all written content is available under the creative commons attribution sharealike 3.0 unported license.

Poster To Download 7 4mb In mathematics, the lambert w function, also called the omega function or product logarithm, [1] is a multivalued function, namely the branches of the converse relation of the function f(w) = we w, where w is any complex number and e w is the exponential function. A list of citizendium articles, and planned articles, about lambert w function. see also changes related to lambert w function , or pages that link to lambert w function or to this page or whose text contains "lambert w function" . In this paper we construct and study in great detail a generalization of the lambert w which involves some special polynomials and even combinatorial aspects. 1. introduction. 1.1. the definition of the lambert w function. the solutions of the tran scendental equation. were studied by euler and by lambert before [7]. Below, we show that the power tower function may be expressed in terms of a function called the lambert w function. the w function has applications in a wide range of areas in pure and applied mathematics.

Lambert W Function From Wolfram Mathworld In this paper we construct and study in great detail a generalization of the lambert w which involves some special polynomials and even combinatorial aspects. 1. introduction. 1.1. the definition of the lambert w function. the solutions of the tran scendental equation. were studied by euler and by lambert before [7]. Below, we show that the power tower function may be expressed in terms of a function called the lambert w function. the w function has applications in a wide range of areas in pure and applied mathematics. Where w −1 is the second branch of the lambert w function [30, 31] and g is given by eq. . (note that for completeness, eq. is added to table 1.) 2.3. evaluating lambert w function. the value of w −1 (x) can be calculated directly using commercial software (such as the productlog[ 1, x] function in mathematica). Called with three arguments w^ { (r)} {k}\!\left (z\right) th derivative of the th branch of the lambert w function, with inherited branch cuts. the following table lists conditions such that is defined in fungrim. an x ray plot illustrates the geometry of a complex analytic function f (z) f. This section has been enlarged. the lambert w function is multi valued and we use the notation w k (x), k ∈ ℤ, for the branches. the original two solutions are identified via wp (x) = w 0 (x) and wm (x) = w − 1 (x 0 i).
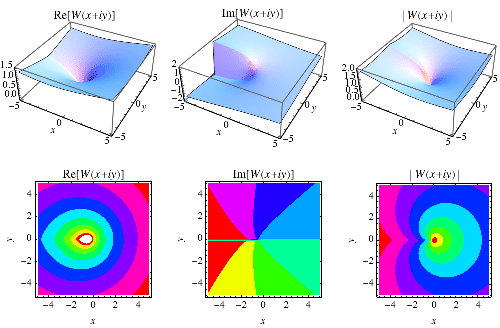
Lambert W Function From Wolfram Mathworld Where w −1 is the second branch of the lambert w function [30, 31] and g is given by eq. . (note that for completeness, eq. is added to table 1.) 2.3. evaluating lambert w function. the value of w −1 (x) can be calculated directly using commercial software (such as the productlog[ 1, x] function in mathematica). Called with three arguments w^ { (r)} {k}\!\left (z\right) th derivative of the th branch of the lambert w function, with inherited branch cuts. the following table lists conditions such that is defined in fungrim. an x ray plot illustrates the geometry of a complex analytic function f (z) f. This section has been enlarged. the lambert w function is multi valued and we use the notation w k (x), k ∈ ℤ, for the branches. the original two solutions are identified via wp (x) = w 0 (x) and wm (x) = w − 1 (x 0 i).
