
Lambert W Function Pdf The lambert w function is to the expression xex what the natural logarithm is to ex: they are both designed to extract from each the value s of x. i intend to present a brief introduction to the lambert w function. (among other sources) do a better job. In mathematics, the lambert w function, also called the omega function or product logarithm, [1] is a multivalued function, namely the branches of the converse relation of the function f(w) = we w, where w is any complex number and e w is the exponential function. the function is named after johann lambert, who considered a related problem in 1758.
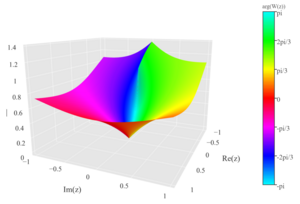
Lambert W Function Wikiwand The lambert w function, also called the omega function, is the inverse function of f(w)=we^w. (1) the plot above shows the function along the real axis. the principal value of the lambert w function is implemented in the wolfram language as productlog[z]. In this video i introduce the lambert w function, and work to demystify it, as well as work through a few simple algebraic examples using it.for videos on ho. The lambert w function, named after johann heinrich lambert [1], is a standard function in both mathematica, where it’s called product log x , and in maple, where you can use both lambert w x or lambert w 0, x . the zero in this latter expression denotes the principal branch of the inverse of x ex . Lambert w function explained. in mathematics, the lambert function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the converse relation of the function, where is any complex number and is the exponential function.

Lambert W Function From Wolfram Mathworld The lambert w function, named after johann heinrich lambert [1], is a standard function in both mathematica, where it’s called product log x , and in maple, where you can use both lambert w x or lambert w 0, x . the zero in this latter expression denotes the principal branch of the inverse of x ex . Lambert w function explained. in mathematics, the lambert function, also called the omega function or product logarithm, is a multivalued function, namely the branches of the converse relation of the function, where is any complex number and is the exponential function. Below, we show that the power tower function may be expressed in terms of a function called the lambert w function. the w function has applications in a wide range of areas in pure and applied mathematics. thus, in addition to being a source of innocent merriment, the power tower function is connected with many important practical problems. The lambert w function is defined to be the multivalued inverse of the function w → we w . it has many applications in pure and applied mathematics, some of which. In this note, we get some explicit approximations for the lambert w function w(x), defined by w(x)e w(x) = x for x ≥ −e −1 . also, we get upper and lower bounds for the hyperpower function. We present a new discussion of the complex branches of w , an asymptotic expansion valid for all branches, an efficient numerical procedure for evaluating the function to arbitrary precision, and a method for the symbolic integration of expressions containing w . 1. introduction.

Lambert W Function From Wolfram Mathworld Below, we show that the power tower function may be expressed in terms of a function called the lambert w function. the w function has applications in a wide range of areas in pure and applied mathematics. thus, in addition to being a source of innocent merriment, the power tower function is connected with many important practical problems. The lambert w function is defined to be the multivalued inverse of the function w → we w . it has many applications in pure and applied mathematics, some of which. In this note, we get some explicit approximations for the lambert w function w(x), defined by w(x)e w(x) = x for x ≥ −e −1 . also, we get upper and lower bounds for the hyperpower function. We present a new discussion of the complex branches of w , an asymptotic expansion valid for all branches, an efficient numerical procedure for evaluating the function to arbitrary precision, and a method for the symbolic integration of expressions containing w . 1. introduction.
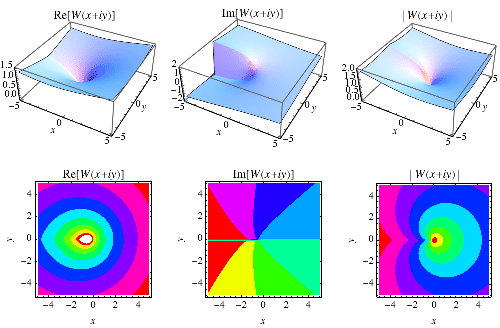
Lambert W Function From Wolfram Mathworld In this note, we get some explicit approximations for the lambert w function w(x), defined by w(x)e w(x) = x for x ≥ −e −1 . also, we get upper and lower bounds for the hyperpower function. We present a new discussion of the complex branches of w , an asymptotic expansion valid for all branches, an efficient numerical procedure for evaluating the function to arbitrary precision, and a method for the symbolic integration of expressions containing w . 1. introduction.
