
Pdf Solutions For Series Of Exponential Equations In Terms Of Lambert I have a function i've been trying to solve of the form: $e^{\alpha t}(\alpha d) = c$, where $\alpha$ is my unknown, $t$ is a time parameter, and $d$ and $c$ are constants. based on what i understand, a good candidate to get an exact solution would be the w lambert function. An introduction to the lambert w function, as well as its application.
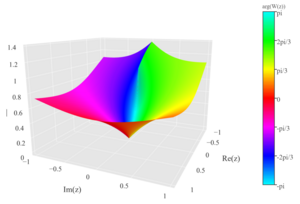
Lambert W Function Wikiwand Lambert’s w function. if you can solve one equation involving exponential functions you can bootstrap your solution solve a lot more equations. the lambert w function is defined to be the function w(x) that maps each x to a solution of the equation. w exp(w) = x. this function is implemented python under scipy.special.lambertw. let’s see. Solving equations with the lambert w function for more info on the lambert w function: introduction video: • lambert w function introduction playlist: • lambert w function. Explore the solutions to exponential equations graphically, numerically, and analytically. discover the analytical solution using the lambert w function and a general numerical solution. uncover the equation linking the fine structure constant to fundamental constants. This is why the lambert w function is a must have algebra tool in you algebra toolbox the lambert w function is a useful tool to solve equations in which the unknown quantity occurs.

Lambert W Function From Wolfram Mathworld Explore the solutions to exponential equations graphically, numerically, and analytically. discover the analytical solution using the lambert w function and a general numerical solution. uncover the equation linking the fine structure constant to fundamental constants. This is why the lambert w function is a must have algebra tool in you algebra toolbox the lambert w function is a useful tool to solve equations in which the unknown quantity occurs. To solve the equation in closed form, we therefore have no choice but to use special functions. the equation isn't in a form to solve it in terms of lambert w. your step x =50−x x = 50 − x is wrong. you could use numerical methods or power series methods. see also wolfram alpha. The lambert function is used to solve equations in which the unknown quantity occurs both in the base and in the exponent, or both inside and outside of a logarithm. the strategy is to convert such an equation into one of the form and then to solve for using the function. Rewrite the equation using the exponential function $e^x$: \[ e^{x \ln 2} = 5 x. \] next bring the equation to the form $y = x e^x$ where $y$ will be a specific number. then we can use the lambert functions to solve this equation.

Lambert W Function From Wolfram Mathworld To solve the equation in closed form, we therefore have no choice but to use special functions. the equation isn't in a form to solve it in terms of lambert w. your step x =50−x x = 50 − x is wrong. you could use numerical methods or power series methods. see also wolfram alpha. The lambert function is used to solve equations in which the unknown quantity occurs both in the base and in the exponent, or both inside and outside of a logarithm. the strategy is to convert such an equation into one of the form and then to solve for using the function. Rewrite the equation using the exponential function $e^x$: \[ e^{x \ln 2} = 5 x. \] next bring the equation to the form $y = x e^x$ where $y$ will be a specific number. then we can use the lambert functions to solve this equation.
