
Largest Subset Of Graph Vertices With Edges Of 2 Or More Colors Given an undirected complete graph with n nodes or vertices. edges of the graph are colored, find the largest subset of vertices with edges of 2 or more colors. we are given graph as adjacency matrix c [] [] where c [i] [j] is color of edge from vertex i to vertex j. since graph is undirected, values c [i] [j] of c [j] [i] are same. In this problem, we are given a complete undirected graph with n nodes or vertices in which the edges of the graph are colored. we are given a graph in the form of an adjacency matrix graph [] [], where graph [i] [j] is the color of the edge from vertex i to vertex j. example 1: input: {2, 0, 3}, {1, 3, 0}} . output:.

Largest Subset Of Graph Vertices With Edges Of 2 Or More Colors Given an undirected complete graph with n nodes or vertices. edges of the graph are colored, find the largest subset of vertices with edges of 2 or more colors. we are given graph as adjacency matrix c[][] where c[i][j] is color of edge from vertex i to vertex j. since graph is undirected, values c. I want to find the subset (of some fixed length) with the greatest sum of edge weights where an edge to a node is only counted once. in other words, in this example the greatest subset of length 2 is {c, d} with a value of 30 34 32 41 20 = 157 (it hits all the values). Coloring edges on a graph s.t. the set of edges for any two vertices have no more than 'k' colors in common. Given an arbitrary (finite) undirected graph, i want to compute a largest possible set of disjoint edges in the graph that is, no two edges in the set share a vertex. i think this should be a standard graph theory problem. is there a good algorithm for this?.

Largest Subset Of Graph Vertices With Edges Of 2 Or More Colors Coloring edges on a graph s.t. the set of edges for any two vertices have no more than 'k' colors in common. Given an arbitrary (finite) undirected graph, i want to compute a largest possible set of disjoint edges in the graph that is, no two edges in the set share a vertex. i think this should be a standard graph theory problem. is there a good algorithm for this?. Let's say you have a graph like this: the largest subset of nodes so that every pair of vertices have an edge between them is $\{3, 5, 7, 12\}$. the second largest subsets are $\{4, 7, 21\}$, $\{3, 5, 7\}$, $\{3, 5, 12\}$, etc. is there an algorithm to find the largest subset efficiently?. Given an undirected complete graph with n nodes or vertices. edges of the graph are colored, find the largest subset of vertices with edges of 2 or more colors. we are given graph as adjacency matrix c[][] where c[i][j] is color of edge from vertex i to vertex j. since graph is undirected, values c[i][j] […]. An isomorphism between two graphs \(g 1\) and \(g 2\) is a bijection \(f:v 1 \to v 2\) between the vertices of the graphs such that \(\{a,b\}\) is an edge in \(g 1\) if and only if \(\{f(a), f(b)\}\) is an edge in \(g 2\text{.}\). It is convenient to represent elements of two given sets by vertices of a graph, with edges between vertices that can be paired. a matching in a graph is a subset of its edges with the property that no two edges share a vertex. a maximum matching—more precisely, a maximum cardinality matching—is a matching with the largest number of edges.
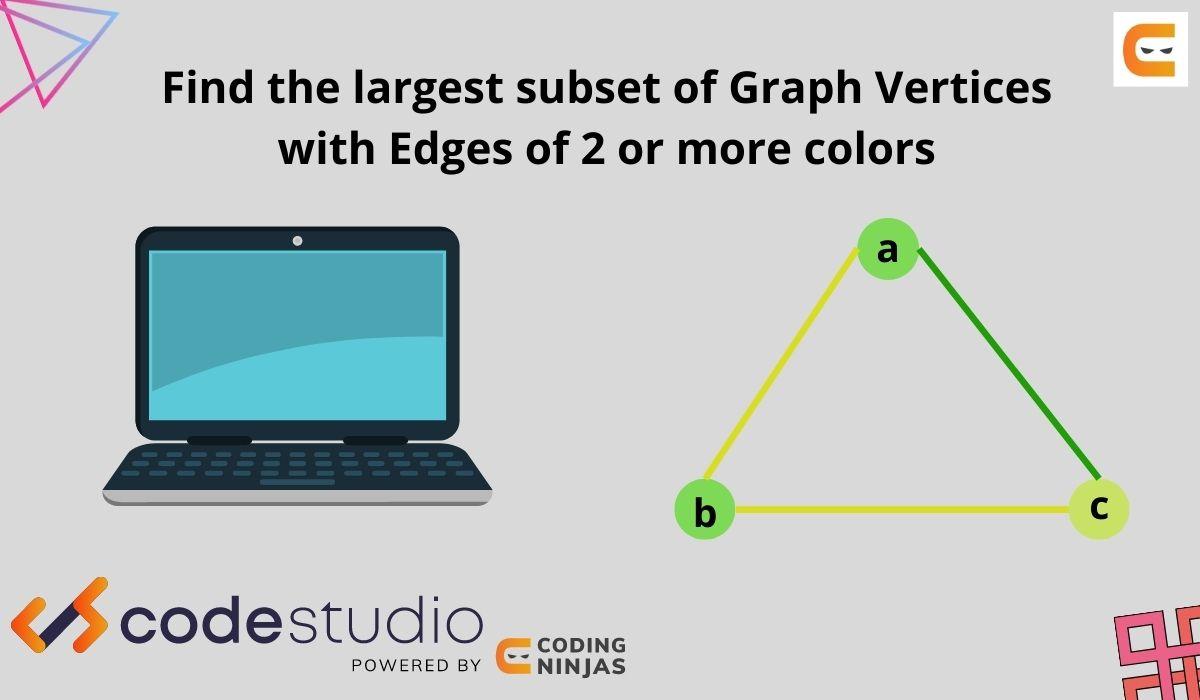
Find The Largest Subset Of Graph Vertices With Edges Of 2 Or More Let's say you have a graph like this: the largest subset of nodes so that every pair of vertices have an edge between them is $\{3, 5, 7, 12\}$. the second largest subsets are $\{4, 7, 21\}$, $\{3, 5, 7\}$, $\{3, 5, 12\}$, etc. is there an algorithm to find the largest subset efficiently?. Given an undirected complete graph with n nodes or vertices. edges of the graph are colored, find the largest subset of vertices with edges of 2 or more colors. we are given graph as adjacency matrix c[][] where c[i][j] is color of edge from vertex i to vertex j. since graph is undirected, values c[i][j] […]. An isomorphism between two graphs \(g 1\) and \(g 2\) is a bijection \(f:v 1 \to v 2\) between the vertices of the graphs such that \(\{a,b\}\) is an edge in \(g 1\) if and only if \(\{f(a), f(b)\}\) is an edge in \(g 2\text{.}\). It is convenient to represent elements of two given sets by vertices of a graph, with edges between vertices that can be paired. a matching in a graph is a subset of its edges with the property that no two edges share a vertex. a maximum matching—more precisely, a maximum cardinality matching—is a matching with the largest number of edges.
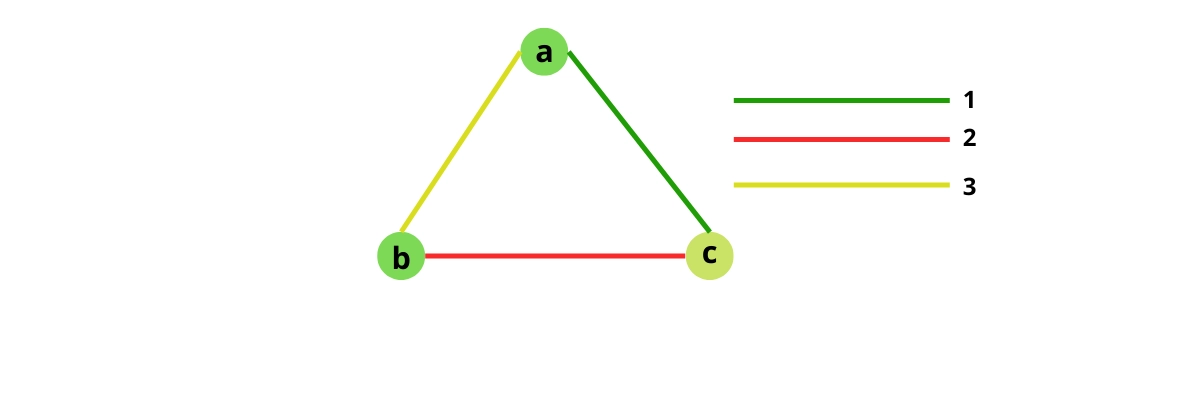
Find The Largest Subset Of Graph Vertices With Edges Of 2 Or More An isomorphism between two graphs \(g 1\) and \(g 2\) is a bijection \(f:v 1 \to v 2\) between the vertices of the graphs such that \(\{a,b\}\) is an edge in \(g 1\) if and only if \(\{f(a), f(b)\}\) is an edge in \(g 2\text{.}\). It is convenient to represent elements of two given sets by vertices of a graph, with edges between vertices that can be paired. a matching in a graph is a subset of its edges with the property that no two edges share a vertex. a maximum matching—more precisely, a maximum cardinality matching—is a matching with the largest number of edges.

Solved 1 How Many Vertices Are There In The Graph How Chegg
