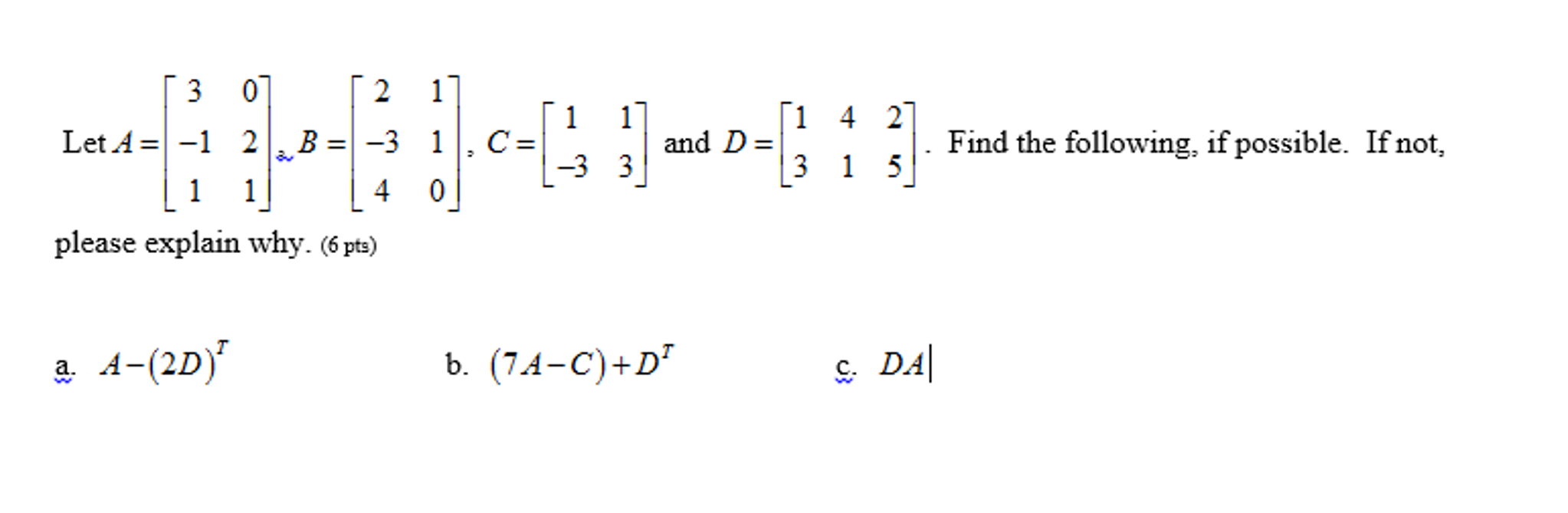
Solved Let A 3 0 1 2 1 1 B 2 1 3 1 4 0 C Chegg Example 18 let a = { 1, 2, 3, 4, 5, 6}, b = { 2, 4, 6, 8 }. find a – b and b – a. a – b = a – (a ∩ b) a ∩ b = {1, 2, 3, 4, 5, 6} ∩ {2, 4, 6, 8} = {2, 4, 6} a – b = a – (a ∩ b) = {1, 2, 3, 4, 5, 6} – {2, 4, 6} = {1, 3, 5} b – a = b – (b ∩ a) = b – (a ∩ b) = {2,. To find the intersection of two sets, we look for elements that are present in both sets. the intersection of sets, denoted as a ∩ b, consists of all elements that belong to both set a and set b. given sets: a = {1, 2, 3, 4, 5} b = {2, 4} step by step process to find a ∩ b: list the elements of set a: 1 ; 2 ; 3 ; 4 ; 5; list the elements of.

Solved Let B 1 2 3 4 5 And Chegg Examples: $\{1,2,3,4,5\} = \{5,2,1,3,4\}$. both are the same sets, defined simply by the elements they contain, and no more. on the other hand, for tuples, the order of elements within the tuple is definitive. The corresponding equivalence relation (which i will write with ∼ ∼) is the one that has 1 ∼ 3 ∼ 5 1 ∼ 3 ∼ 5 and 4 ∼ 6 4 ∼ 6. Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. x − 3 y 2 z = − 1 not the question you’re looking for? post any question and get expert help quickly. {1, 3}, {2, 4, 5}, {6} explanation: for the partition sub sets to be an equivalence relation, the following conditions must be met: the partition sub sets must be distinct, meaning they must not share any entries.

Solved 1 Let A1 1 2 3 4 A2 0 1 2 A3 1 0 1 And Let Chegg Enhanced with ai, our expert help has broken down your problem into an easy to learn solution you can count on. here’s the best way to solve it. x − 3 y 2 z = − 1 not the question you’re looking for? post any question and get expert help quickly. {1, 3}, {2, 4, 5}, {6} explanation: for the partition sub sets to be an equivalence relation, the following conditions must be met: the partition sub sets must be distinct, meaning they must not share any entries. Find f −1 if it exists : f : a → b, where a = {0, −1, −3, 2}; b = {−9, −3, 0, 6} and f(x) = 3 x. consider f : r → r given by f ( x ) = 4 x 3. show that f is invertible. Using the standard basis b {1}=\left\{1, x, let t: r^3 → r^3 be defined by t[x y z] = [2x y 3z 4x 2y 6z 6x 3y 9z]. find at, ker t, range t, v(t), and p(t). Ex 1.2, 6 let a = {1, 2, 3}, b = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from a to b. show that f is one one. a = {1, 2, 3}, b = {4, 5, 6, 7}. f = {(1, 4), (2, 5), (3, 6)}. since every element of a has a unique image. hence , f is one one. Example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. find a × (b ∩ c) b ∩ c = {3, 4} ∩ {"4, 5, 6" } = {"4" } a × (b ∩ c) = {"1, 2, 3" } × {"4" } = {" (1, 4), (2, 4), (3, 4)" } ∩ intersection : common between two sets example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}.

Solved Let A 1 1 2 3 4 A 2 0 1 2 A 3 1 Chegg Find f −1 if it exists : f : a → b, where a = {0, −1, −3, 2}; b = {−9, −3, 0, 6} and f(x) = 3 x. consider f : r → r given by f ( x ) = 4 x 3. show that f is invertible. Using the standard basis b {1}=\left\{1, x, let t: r^3 → r^3 be defined by t[x y z] = [2x y 3z 4x 2y 6z 6x 3y 9z]. find at, ker t, range t, v(t), and p(t). Ex 1.2, 6 let a = {1, 2, 3}, b = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from a to b. show that f is one one. a = {1, 2, 3}, b = {4, 5, 6, 7}. f = {(1, 4), (2, 5), (3, 6)}. since every element of a has a unique image. hence , f is one one. Example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. find a × (b ∩ c) b ∩ c = {3, 4} ∩ {"4, 5, 6" } = {"4" } a × (b ∩ c) = {"1, 2, 3" } × {"4" } = {" (1, 4), (2, 4), (3, 4)" } ∩ intersection : common between two sets example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}.
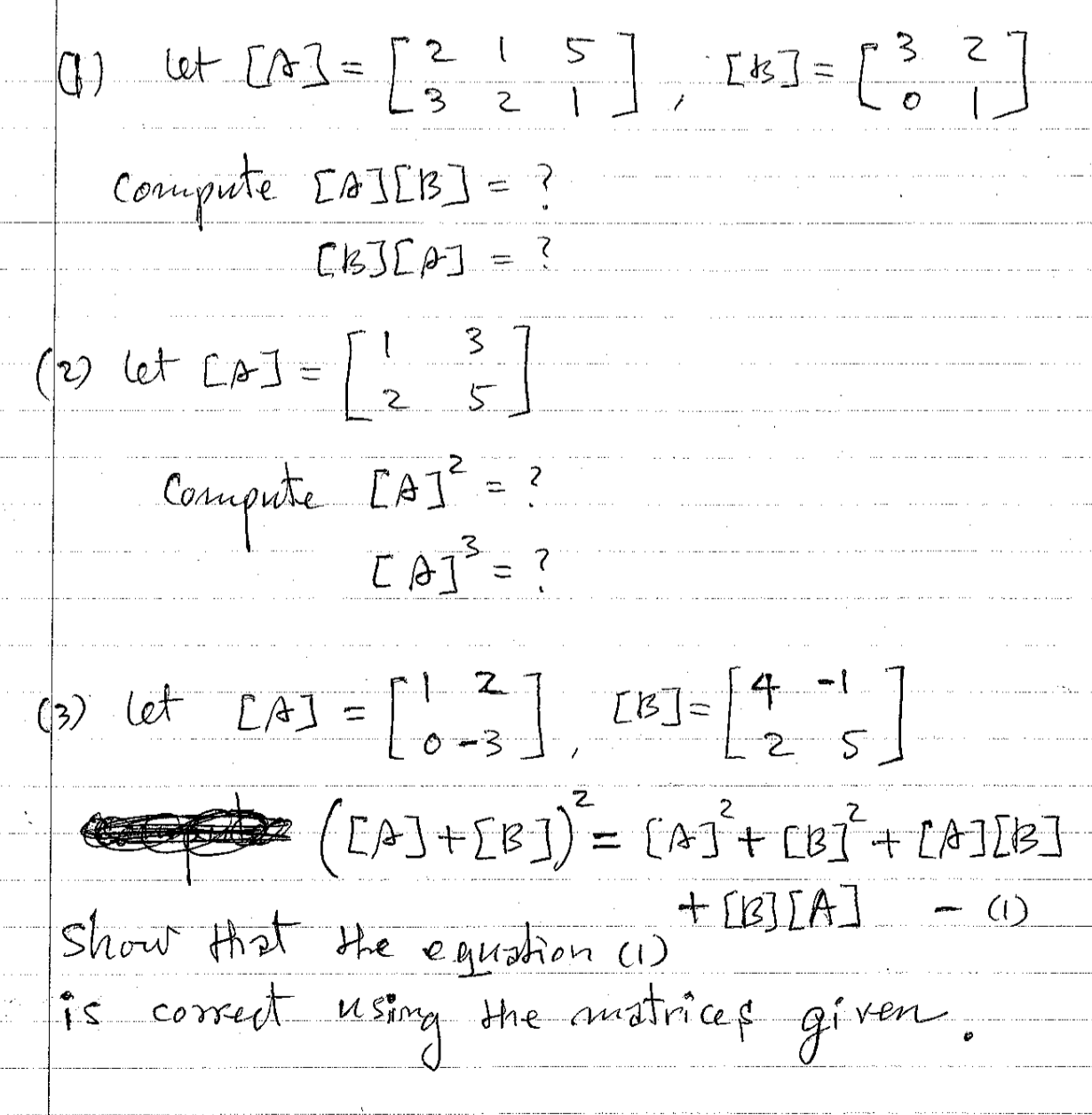
Solved Let A 2 1 5 3 2 1 B 3 2 0 1 Compute Chegg Ex 1.2, 6 let a = {1, 2, 3}, b = {4, 5, 6, 7} and let f = {(1, 4), (2, 5), (3, 6)} be a function from a to b. show that f is one one. a = {1, 2, 3}, b = {4, 5, 6, 7}. f = {(1, 4), (2, 5), (3, 6)}. since every element of a has a unique image. hence , f is one one. Example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. find a × (b ∩ c) b ∩ c = {3, 4} ∩ {"4, 5, 6" } = {"4" } a × (b ∩ c) = {"1, 2, 3" } × {"4" } = {" (1, 4), (2, 4), (3, 4)" } ∩ intersection : common between two sets example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}.

Solved Let A 1 2 2 3 3 4 4 5 Determine Chegg
