Let Yyx Be The Solution Of The Differential Equation X2 3y2dx3xydy0 Y11 Then 6y2e

Let Y X Be The Solution Of The Differential Equation Sarthaks .let `y=y (x)` be the solution of the dif to solve the given differential equation and find the value of |(y(2))3−12y(2)|, we will follow these steps: let y = vx, where v is a function of x. then, we have: this can be simplified further. this will yield a logarithmic function on the right side. Let $$y=y (x)$$ be the solution of the differential equation $$\frac {d y} {d x}=\frac { (\tan x) y} {\sin x (\sec x \sin x \tan x)}, x \in\left (0, \frac {\pi} {2}\right)$$ satisfying the condition $$y\left (\frac {\pi} {4}\right)=2$$.

Bs Grewal Solutions Solve X 2 Y 2 A 2 Xdx X 2 Y 2 B 2 Ydy 0 Let y = y (x) be the solution of the differential equation (x2 – 3y2)dx 3xy dy = 0, y (1) = 1. then 6y2(e) is equal to (1) 3e2 (2) e2 (3) 2e2 (4) 3e2 2. To solve the given differential equation, we first rewrite it in a more manageable form. the equation is given as: x(x2 ex)dy (ex(x−2)y−x3)dx =0. we can rearrange this to isolate dy dx: dy dx = − x(x2 ex)ex(x−2)y−x3. next, we can separate the variables: ex(x−2)y−x3dy = −x(x2 ex)dx. now we integrate both sides. If the line x=1 x = 1 intersects the curve y=y (x) y = y(x) at y=2 y = 2 and the line x=2 x = 2 intersects the curve y=y (x) y = y(x) at y=\alpha y = α, then a value of \alpha α is :. We know that the integrating factor of the linear differential equation d y d x p (x) y = q (x) is given by i f = e ∫ p (x) d x. we know that if ∫ f (x) d x = u (x) and d d x g (x) = v (x), then ∫ f (x) g (x) d x = g (x) u (x) − ∫ u (x) v (x) d x. this is known as integration by parts.

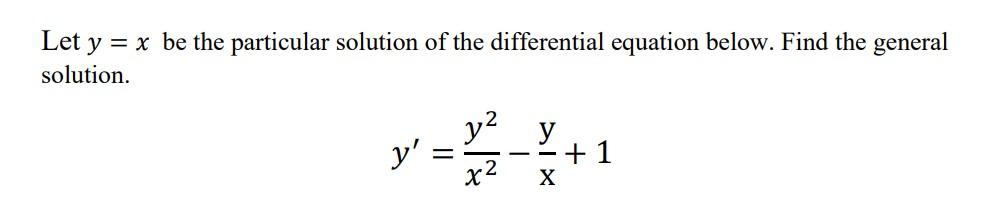
Solved Let Y X Be The Particular Solution Of The Chegg If the line x=1 x = 1 intersects the curve y=y (x) y = y(x) at y=2 y = 2 and the line x=2 x = 2 intersects the curve y=y (x) y = y(x) at y=\alpha y = α, then a value of \alpha α is :. We know that the integrating factor of the linear differential equation d y d x p (x) y = q (x) is given by i f = e ∫ p (x) d x. we know that if ∫ f (x) d x = u (x) and d d x g (x) = v (x), then ∫ f (x) g (x) d x = g (x) u (x) − ∫ u (x) v (x) d x. this is known as integration by parts. To apply the initial condition, substitute x = 2 and y = 2 3 into the derived general solution. this would then allow us to solve for any constants and verify that the solution meets the given conditions. substitution is a technique for simplifying complex differential equations. When n = 1 the equation can be solved using separation of variables. for other values of n we can solve it by substituting u = y1−n and turning it into a linear differential equation (and then solve that). To solve the given differential equation, we will use the method of separation of variables and then apply the initial condition to find the particular solution. To solve the differential equation dy dx = 1 xey−x with the initial condition y(0) = 0 and find the minimum value of y(x) over the interval (−√2,√2), we can follow these steps:.

Let Y Y X Be The Solution Of The Differential Equation X 2 1 To apply the initial condition, substitute x = 2 and y = 2 3 into the derived general solution. this would then allow us to solve for any constants and verify that the solution meets the given conditions. substitution is a technique for simplifying complex differential equations. When n = 1 the equation can be solved using separation of variables. for other values of n we can solve it by substituting u = y1−n and turning it into a linear differential equation (and then solve that). To solve the given differential equation, we will use the method of separation of variables and then apply the initial condition to find the particular solution. To solve the differential equation dy dx = 1 xey−x with the initial condition y(0) = 0 and find the minimum value of y(x) over the interval (−√2,√2), we can follow these steps:.