Linear Algebra Solution 18 Png Etape 1 1 Sur 2 Let V R A1 A2

Linear Algebra Solution Set By A P Singh Pdf View linear algebra solution 18 from math 251 at concordia university. etape 1 1 sur 2 let v = r? : (a1,a2) (b1, b2) = (a1 2by,as 3b2) o :c (ay,ay) = (cay,cas) for v to be a vector space. Find step by step solutions and answers to exercise 18 from linear algebra 9780134876979, as well as thousands of textbooks so you can move forward with confidence.

Linear Algebra Lect 2 Pdf Vector Space Basis Linear Algebra If t = t 2 , then we have v = {y ∶ t (y) = y} n (t ) since x = t (x) (x − t (x)) and we have t (t (x)) = t (x) and t (x − t (x)) = t (x) − t (x) = 0. First suppose that is finite dimensional, so that it is spanned by some list 1, , , and let 1, 2, be any sequence of vectors in ; by 2.22, the list 1, 2, , 1 must be linearly dependent. Gilbert strang, introduction to linear algebra, 6th edition (2023) 1. when can lines of lengths r,s,t form a triangle? they must satisfy the strict triangle inequalities r < s t s < r t t < r s if we allow equality, the triangle will have angles of 0,0 and 180 degrees. if r > s t, then one segment r is too long to complete a triangle. 2. Since e is an idempotent linear operator it is diagonalizable by question 4. so there exists a basis of v consisting of characteristics vectors of e corresponding to the characteristic values 0 and 1.

Solved Linear Algebra Let S 1 1 1 1 2 3 1 0 Chegg Gilbert strang, introduction to linear algebra, 6th edition (2023) 1. when can lines of lengths r,s,t form a triangle? they must satisfy the strict triangle inequalities r < s t s < r t t < r s if we allow equality, the triangle will have angles of 0,0 and 180 degrees. if r > s t, then one segment r is too long to complete a triangle. 2. Since e is an idempotent linear operator it is diagonalizable by question 4. so there exists a basis of v consisting of characteristics vectors of e corresponding to the characteristic values 0 and 1. The five linear equations in five unknowns, if solved simultaneously, produce the unique solution: a = 4, t = 5, h = 7, w = 6 and e = 2, so that the original example in addition was 47474 5272 = 52746. To deter mine formulas for f1,f2,f3 we seek functionals f1(»1; »2; »3) = a1»1 a2»2 a3»3, f2(»1; »2; »3) = b1»1 b2»2 b3»3, and f3(»1; »2; »3) = c1»1 c2»2 c3»3 such that fi(xj) = ±ij. I do not understand the textbook's solution and would greatly appreciate it if people could please take the time to review mine. if there is anything wrong with my reasoning, please specify why and what the correct solution is. Let w1 and w2 be subspaces of a vector space v . prove that w1 w2 is a subspace of v that contains both w1 and w2. prove that any subspace of v that contains both w1 and w2 must also contain w1 w2. show that a subset w of a vector space v is a subspace of v if and only if span(w ) = w .

Linear Algebra Solution 18 Png Etape 1 1 Sur 2 Let V R A1 A2 The five linear equations in five unknowns, if solved simultaneously, produce the unique solution: a = 4, t = 5, h = 7, w = 6 and e = 2, so that the original example in addition was 47474 5272 = 52746. To deter mine formulas for f1,f2,f3 we seek functionals f1(»1; »2; »3) = a1»1 a2»2 a3»3, f2(»1; »2; »3) = b1»1 b2»2 b3»3, and f3(»1; »2; »3) = c1»1 c2»2 c3»3 such that fi(xj) = ±ij. I do not understand the textbook's solution and would greatly appreciate it if people could please take the time to review mine. if there is anything wrong with my reasoning, please specify why and what the correct solution is. Let w1 and w2 be subspaces of a vector space v . prove that w1 w2 is a subspace of v that contains both w1 and w2. prove that any subspace of v that contains both w1 and w2 must also contain w1 w2. show that a subset w of a vector space v is a subspace of v if and only if span(w ) = w .

Solved Problem 1 1 Linear Algebra 22pts Let V1 Chegg I do not understand the textbook's solution and would greatly appreciate it if people could please take the time to review mine. if there is anything wrong with my reasoning, please specify why and what the correct solution is. Let w1 and w2 be subspaces of a vector space v . prove that w1 w2 is a subspace of v that contains both w1 and w2. prove that any subspace of v that contains both w1 and w2 must also contain w1 w2. show that a subset w of a vector space v is a subspace of v if and only if span(w ) = w .
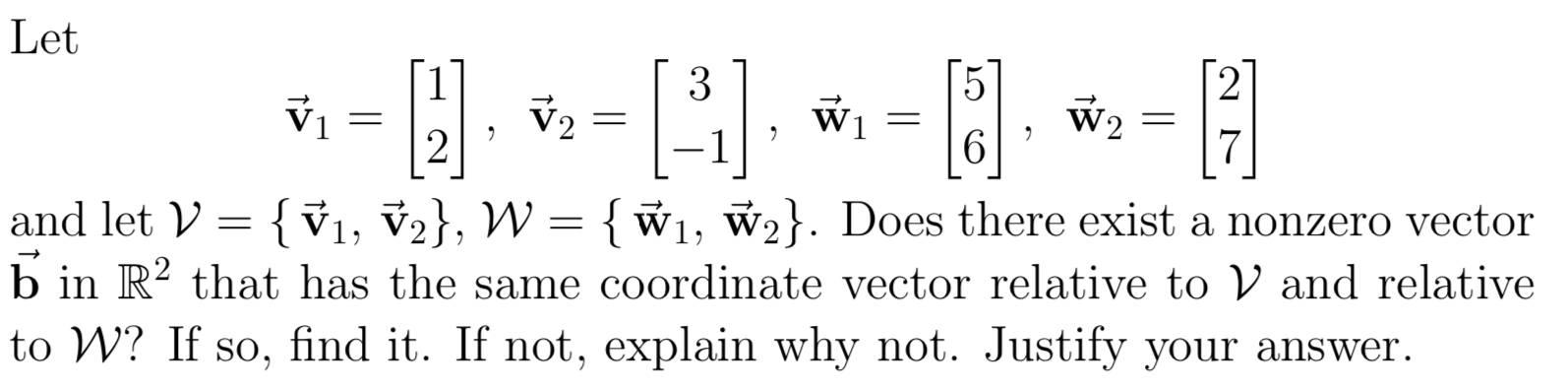
Solved Linear Algebra Let фџ ђ1фџ ѓ фџ ђ3фџ ѓ фџ ђ5фџ ѓ фџ ђ2фџ ѓ вѓ V 1 2 Chegg
Comments are closed.