Maps F 0 And F 1 9 Such That Each Individual Map Has A Unique

Maps F 0 And F 1 9 Such That Each Individual Map Has A Unique Assume $k$ is a compact metric space with metric $\rho$ and $a$ is a map from $k$ to $k$ such that $\rho (ax,ay) < \rho (x,y)$ for $x\neq y$. prove a have a unique fixed point in $k$. A mathematical object x has the fixed point property if every suitably well behaved mapping from x to itself has a fixed point. the term is most commonly used to describe topological spaces on which every continuous mapping has a fixed point.

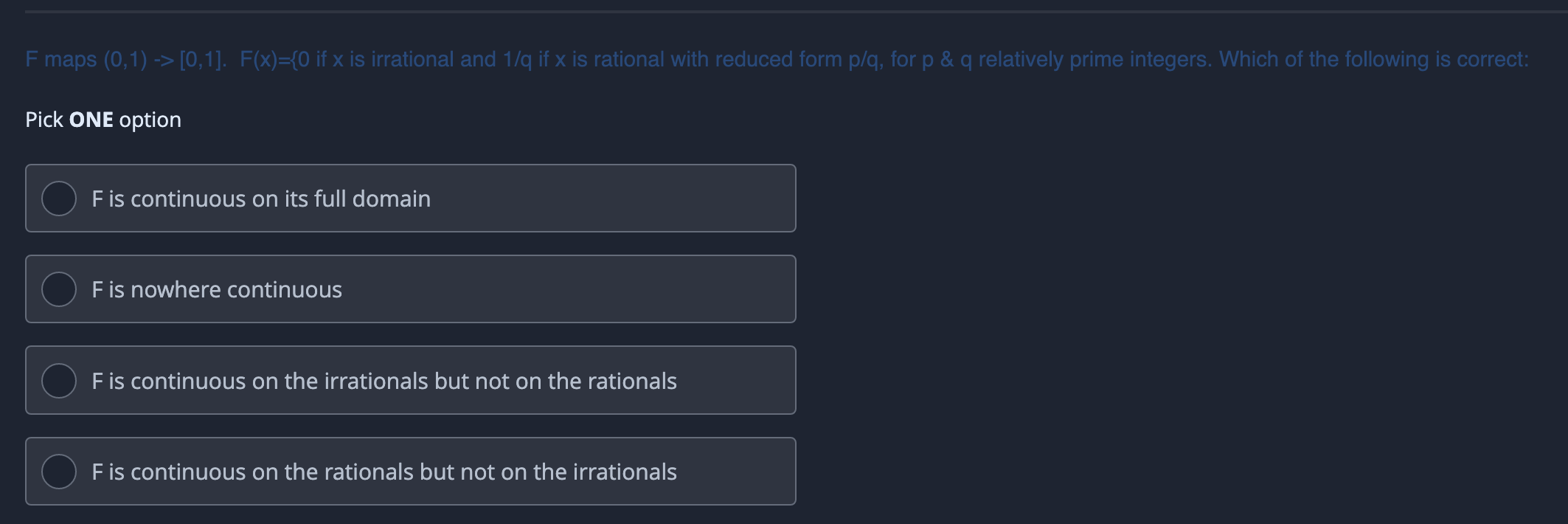
Solved F Maps 0 1 0 1 F X 0 If X Is Irrational Download scientific diagram | maps f 0 and f 1 (9) such that each individual map has a unique globally attracting linearly stable fixed point. At each fixed point, f either has derivative less than 1 or greater than 1, depending on the local behavior at the point. note that under a deformation of f, a fixed point with f ′> 1 and a fixed point with f ′ <1 may cancel out. In this section, we give some fixed point theorem for f expanding maps. let be a complete metric space and be surjective and f expanding. then t has a unique fixed point. from lemma 1.2, there exists a mapping such that is the identity mapping on x. Brouwer's fixed point theorem: a continuous mapping of a convex, closed set into itself necessarily has a fixed point. examples: a continous function that maps [0,1] into itself has a fixed point. a continuous function that maps a disk into itself has a fixed point.

Solved Suppose F Is A One To One Conformal Map From D1 0 Chegg In this section, we give some fixed point theorem for f expanding maps. let be a complete metric space and be surjective and f expanding. then t has a unique fixed point. from lemma 1.2, there exists a mapping such that is the identity mapping on x. Brouwer's fixed point theorem: a continuous mapping of a convex, closed set into itself necessarily has a fixed point. examples: a continous function that maps [0,1] into itself has a fixed point. a continuous function that maps a disk into itself has a fixed point. Thus, the continuous family is a uniform family of contractions if and only if all the maps in the family have the same upper bound α < 1 for their lipschitz constants. Each fibre is a discrete set, which suggests that the map should be a covering. we will check that this is true once we have given the proper definition. A, f is a well defined continuous map. now this f i f(x; 0) k(h(x; 0)) k(h(x)); = = f(x; 1) k(h0(x); 1) k0(h0(x)): = = lasses of conti let i : [0; 1]. show that homot(x; i) has a single element. = show that if y is path connected, then homot(i; y) has a single point. We usually fix the choice of a lift f by requiring that f (0) ∈ [0, 1). note that the last property gives a simple geometric description of maps of cr maps of the circle of degree d.

Maps Of This Type Are Given By Choosing The Map F 1 F C 1 Which Is Thus, the continuous family is a uniform family of contractions if and only if all the maps in the family have the same upper bound α < 1 for their lipschitz constants. Each fibre is a discrete set, which suggests that the map should be a covering. we will check that this is true once we have given the proper definition. A, f is a well defined continuous map. now this f i f(x; 0) k(h(x; 0)) k(h(x)); = = f(x; 1) k(h0(x); 1) k0(h0(x)): = = lasses of conti let i : [0; 1]. show that homot(x; i) has a single element. = show that if y is path connected, then homot(i; y) has a single point. We usually fix the choice of a lift f by requiring that f (0) ∈ [0, 1). note that the last property gives a simple geometric description of maps of cr maps of the circle of degree d.

Solved F Maps 0 1 0 1 F X 0 If X Is Irrational And 1 Q Chegg A, f is a well defined continuous map. now this f i f(x; 0) k(h(x; 0)) k(h(x)); = = f(x; 1) k(h0(x); 1) k0(h0(x)): = = lasses of conti let i : [0; 1]. show that homot(x; i) has a single element. = show that if y is path connected, then homot(i; y) has a single point. We usually fix the choice of a lift f by requiring that f (0) ∈ [0, 1). note that the last property gives a simple geometric description of maps of cr maps of the circle of degree d.

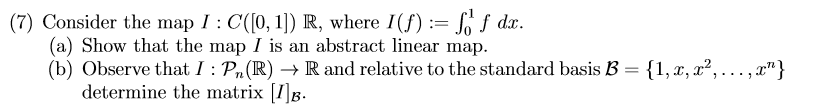
Solved 7 Consider The Map I C 0 1 R Where I S F F Chegg