
Permutation Group Pdf Permutation Group Mathematics Mathematically the rubik's cube is a permutation group. it has 6 different colors and each color is repeated exactly 9 times, so the cube can be considered as an ordered list which has 54 elements with numbers between 1 and 6, each number meaning a color being repeated 9 times. We first define some properties of cube group elements, and then use these properties and what we learned above to develop some macros or combina tions of cube moves that will help us accomplish specific cubie rearrangements that will enable us to solve the cube.

Mathematics Of The Rubik S Cube Permutation Group The rubik's cube group is the subgroup of the symmetric group generated by the six permutations corresponding to the six clockwise cube moves. with this construction, any configuration of the cube reachable through a sequence of cube moves is within the group. Ng each cubie to its original con guration. the rubik's cube exhibits a group structure, which makes it a great tool for. understanding group theory {and vice versa. its structure and non trivial complexity (size) amenable to advan. The rubik's cube; the decomposition of the f turn is shown in figure 4. the turn decomposes into two isjoint 4 cycles, which permute the edges and the corners independently. since a 4 cycle is odd, the total permutation of. Weighted permutations and the group of the rubik's cube by kung sing shih a)a) abstract. the group of rubik's cube is shown to be a subdirect product of its vertex group and edge group, both of which semi direct products. weighted permutations and their composition rule have been introduced for the purpose. this theoretical establishment and method.
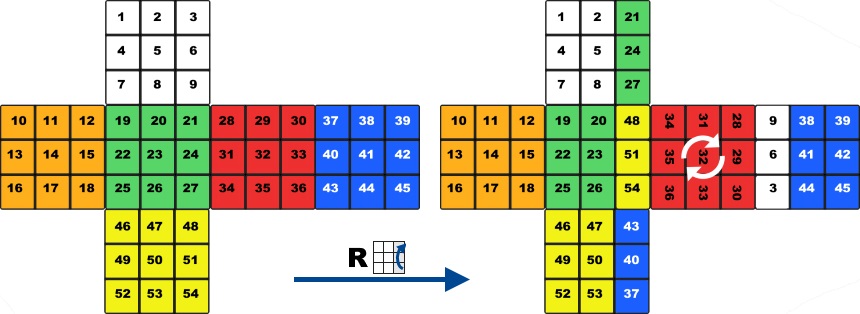
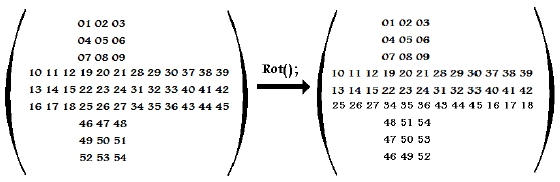
Mathematics Of The Rubik S Cube Permutation Group The rubik's cube; the decomposition of the f turn is shown in figure 4. the turn decomposes into two isjoint 4 cycles, which permute the edges and the corners independently. since a 4 cycle is odd, the total permutation of. Weighted permutations and the group of the rubik's cube by kung sing shih a)a) abstract. the group of rubik's cube is shown to be a subdirect product of its vertex group and edge group, both of which semi direct products. weighted permutations and their composition rule have been introduced for the purpose. this theoretical establishment and method. Constructed the rubik's cube group. the rubik's cube group was shown to be g = hr; b; l; u f; di, which is a subgroup of s54. the first and second fundamental theo rems of cube theory were presented, which gave the criteria for all the possible arrange. The number of possible permutations of the squares on a rubik’s cube seems daunting. there are 8 corner pieces that can be arranged in 8! ways, each of which can be arranged in 3 orientations, giving 38 possibilities for each permutation of the corner pieces. F permutations. if one imagines this diagram folded into the shape of a cube, one can see how each cubie has two or three facelets. for example, the cubie where the up, front, and left faces meet has facelet. A very important class of groups are so called permutation groups which are very closely related to rubik’s cube. thus, in addition to being a fiendishly difficult puzzle, rubik’s cube provides many concrete examples of groups and of applications of group theory.

Permutation Group Pdf Group Mathematics Permutation Constructed the rubik's cube group. the rubik's cube group was shown to be g = hr; b; l; u f; di, which is a subgroup of s54. the first and second fundamental theo rems of cube theory were presented, which gave the criteria for all the possible arrange. The number of possible permutations of the squares on a rubik’s cube seems daunting. there are 8 corner pieces that can be arranged in 8! ways, each of which can be arranged in 3 orientations, giving 38 possibilities for each permutation of the corner pieces. F permutations. if one imagines this diagram folded into the shape of a cube, one can see how each cubie has two or three facelets. for example, the cubie where the up, front, and left faces meet has facelet. A very important class of groups are so called permutation groups which are very closely related to rubik’s cube. thus, in addition to being a fiendishly difficult puzzle, rubik’s cube provides many concrete examples of groups and of applications of group theory.
Mathematics Of The Rubiks Cube Permutation Group F permutations. if one imagines this diagram folded into the shape of a cube, one can see how each cubie has two or three facelets. for example, the cubie where the up, front, and left faces meet has facelet. A very important class of groups are so called permutation groups which are very closely related to rubik’s cube. thus, in addition to being a fiendishly difficult puzzle, rubik’s cube provides many concrete examples of groups and of applications of group theory.
