Matrix Multiplication Linear Combinations And Parameters

Matrix Multiplication Pdf Matrix Mathematics System Of Linear In this video, i go over the solutions to week 2 lab problems. we'll talk about rules for matrix addition subtraction and multiplication and finding linear c. The previous section introduced vectors and linear combinations and demonstrated how they provide a way to think about linear systems geometrically. in particular, we saw that the vector b is a linear combination of the vectors v 1, v 2,, v n precisely when the linear system corresponding to the augmented matrix.
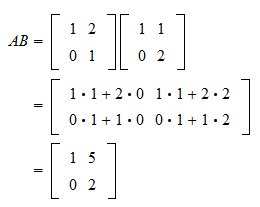
Matrix Multiplication And Linear Combinations The product of a matrix a by a vector y will be the linear combination of the columns of a using the components of y as weights. if a is an mxn matrix, a = [v → 1 v → 2 v → n], then x → must be an n dimensional vector, and the product a x → will be an m dimensional vector. Understand how the product of a matrix and a vector can be expressed as a linear combination of its columns or rows. In general, any sub block structure consistent with matrix multiplication (more formally, \ (a\) and \ (b\) are conformable for multiplication) is fine. in particular, the blocks do not have to be square. While a matrix equation is indeed equivalent to a vector equation, the question a matrix equation naturally asks is not one about linear combinations. instead, we can (and will) think of matrix multiplication as a function which transforms an input vector into an output vector.
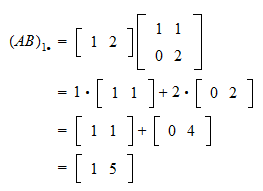
Matrix Multiplication And Linear Combinations In general, any sub block structure consistent with matrix multiplication (more formally, \ (a\) and \ (b\) are conformable for multiplication) is fine. in particular, the blocks do not have to be square. While a matrix equation is indeed equivalent to a vector equation, the question a matrix equation naturally asks is not one about linear combinations. instead, we can (and will) think of matrix multiplication as a function which transforms an input vector into an output vector. My confusion here is in matrix ab, in my view, the rows of ab are looking like a linear combination of columns of matrix b and coefficients are from matrix a. i define it like for matrix a above. The next important matrix operation we will explore is multiplication of matrices. the operation of matrix multiplication is one of the most important and useful of the matrix operations. It is helpful to see the geometric picture in these small cases, because the goal of linear algebra is to deal with very large matrices, like 1000 by 100. (that's actually a pretty small matrix.). Activity 2.2.0.1. use the definition of matrix multiplication to find the product of a matrix and a vector.
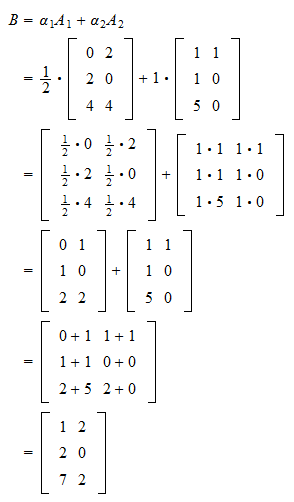
Linear Combinations My confusion here is in matrix ab, in my view, the rows of ab are looking like a linear combination of columns of matrix b and coefficients are from matrix a. i define it like for matrix a above. The next important matrix operation we will explore is multiplication of matrices. the operation of matrix multiplication is one of the most important and useful of the matrix operations. It is helpful to see the geometric picture in these small cases, because the goal of linear algebra is to deal with very large matrices, like 1000 by 100. (that's actually a pretty small matrix.). Activity 2.2.0.1. use the definition of matrix multiplication to find the product of a matrix and a vector.
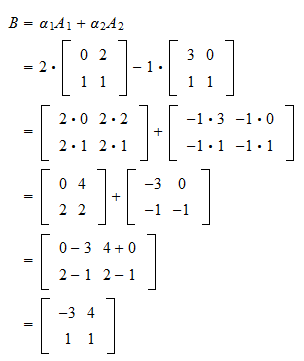
Linear Combinations It is helpful to see the geometric picture in these small cases, because the goal of linear algebra is to deal with very large matrices, like 1000 by 100. (that's actually a pretty small matrix.). Activity 2.2.0.1. use the definition of matrix multiplication to find the product of a matrix and a vector.
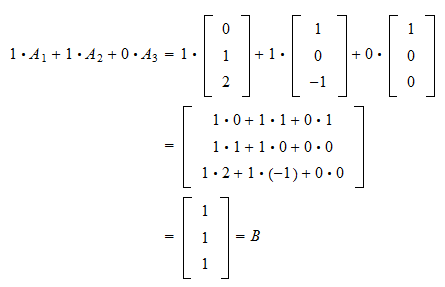
Linear Combinations
Comments are closed.