
Mit Integration Bee 2020 Problem 1 Integrity Problem Elementary 1 1= p 2 arcsin(x) x3 dx= 1=2 12 z ˇ=2 0 sin(2x)cos(cos(x))dx= 2(cos(1) sin(1) 1) 13 z 2ˇ 0 sin(sin(x) x)dx= 0 14 z 1 x 20191 p 2018 k=0 (k 1)x k p k=0 x k dx= log(1 2020x ) 15 z ˇ 2 0 1 tan p 2020(x) 1 dx= ˇ=4 16 z x(1 x)2020 dx= (1 x)2022 2022 (1 2021x) 2021 17 z sec4(x)tan(x) sec4(x) 4 dx= 1 4 log sec4(x) 4 18 z x2x(2log(x) 2)dx= x2x. In this post, we will explore solutions to several problems from the 2020 mit integration bee qualifier exam, demonstrating various integration techniques. problem 1: integral of logarithmic functions problem statement. evaluate the integral: [ i = \\int {e}^{e^e} \\frac{\\log x}{x} , dx ] solution.

Mit Integration Bee Finals Problem 2 By Complexbulb Medium We show in this video some tips and tricks to evaluate the first 5 integrals in the mit integration bee qualifying exam in january 2020. for more math stuff,. We solve the first 10 of 20 problems in teh mit 2020 integration bee qualifying exams. the problems are relatively easy we hope you enjoy following along. In the first chapter of this book, there is a review of the basic integration formulas, and techniques such as integration by substitution, integration by parts, trigonometric and hyperbolic. Finals problem 1 z ex 2cosx 3 mit integration bee: finals tiebreakers (time limit per integral: 5 minutes) finals tiebreakers problem 1 z dx 4 p x4 1. finals tiebreakers problem 1 z dx 4 p x4 1 = 1 2 arctan x 4 p 1 x4! 1 4 log 4 p 1 x4 x 4 p.
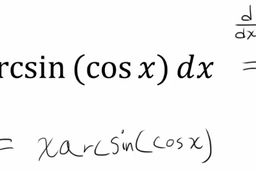
Video Math Tutorial How To Solve 29 Typical Mit Integration Bee In the first chapter of this book, there is a review of the basic integration formulas, and techniques such as integration by substitution, integration by parts, trigonometric and hyperbolic. Finals problem 1 z ex 2cosx 3 mit integration bee: finals tiebreakers (time limit per integral: 5 minutes) finals tiebreakers problem 1 z dx 4 p x4 1. finals tiebreakers problem 1 z dx 4 p x4 1 = 1 2 arctan x 4 p 1 x4! 1 4 log 4 p 1 x4 x 4 p. University of alberta integration bee 2020 presented by the mathematical sciences society. there are a couple of ways to solve this problem i will propose a few below. therefore this becomes basically the gamma function evaluated at 2021. (2021) = 2020! 1 = 2020! from above = 2020!. Mit integration bee 2020 problem 1 let solve. skip to content. The mit integration bee is an annual integral calculus competition pioneered in 1981 by the massachusetts institute of technology. more. problem source:. Semifinal #1 problem 4 z5 2 2 (x 3−3x) −3(x −3x) √ x2 −4 dx = 2 9−2− 9. mit integration bee: semifinal # 2 (time limit per integral: 3 minutes) semifinal # 2 problem 1 z1.
