Mit Integration Bee 2024 Maths Mathematics Mitintegrationbee R Mit integration bee: semifinal #2 (time limit per integral: 4 minutes) z ∞ sin(x) sin(2x) sin(3x) dx. Solving all the integrals from the 2024 mit integration bee finals maths 505 67.4k subscribers subscribed.
Mit 2024 Integration Bee Semi Finals Problem By Wojciech Kowalczyk Want to test your own integration skills? set a timer for 20 minutes and take the 2024 qualifier test. then check your work here. In this article, we look at a problem from the semi finals of the 2024 bee. the thing that is particularly fascinating about this bee is that rather than being difficulty based, it is speed. Therefore, we need to discuss different cases to apply the residue theorem. (a) when > 1, we have | 1| > 1 and | 2| < 1. 1 2 1 2 − 1 . when > 1. −1, we have | 1| < 1 and | 2| > 1. − 1 2 2 − 1 when < −1. (c) when −1 ≤ ≤ 1, the integral does not converge. = sin2 (2 ) cos2 (3 ) d − sin2 (2 ) cos2 (3 ) d. → ∞ according to the mean value theorem. He will be accompanied by evan chen, a graduate student (and undergraduate alum) from mit mathematics, and a former deputy leader of the usa international math olympiad team.
Mit 2024 Integration Bee Semi Finals Problem By Wojciech Kowalczyk Therefore, we need to discuss different cases to apply the residue theorem. (a) when > 1, we have | 1| > 1 and | 2| < 1. 1 2 1 2 − 1 . when > 1. −1, we have | 1| < 1 and | 2| > 1. − 1 2 2 − 1 when < −1. (c) when −1 ≤ ≤ 1, the integral does not converge. = sin2 (2 ) cos2 (3 ) d − sin2 (2 ) cos2 (3 ) d. → ∞ according to the mean value theorem. He will be accompanied by evan chen, a graduate student (and undergraduate alum) from mit mathematics, and a former deputy leader of the usa international math olympiad team. In going from $ (2)$ to $ (3)$, we used a well known integral representation of the beta function. This is a brief guide to the problems i’ve solved on the 2024 mit integration bee qualifying exam. these solutions are by no means the only way of solving the listed problems or the optimal solutions. The integrals and answers can be found at math.mit.edu ~yyao1 pdf 2024 semifinal.pdfplaylist for the full event: playlist?lis. The document describes the problems for the finals of the mit integration bee. it contains 5 problems testing various integration techniques like trigonometric substitution and partial fractions.
Mit 2024 Integration Bee Semi Finals Problem By Wojciech Kowalczyk In going from $ (2)$ to $ (3)$, we used a well known integral representation of the beta function. This is a brief guide to the problems i’ve solved on the 2024 mit integration bee qualifying exam. these solutions are by no means the only way of solving the listed problems or the optimal solutions. The integrals and answers can be found at math.mit.edu ~yyao1 pdf 2024 semifinal.pdfplaylist for the full event: playlist?lis. The document describes the problems for the finals of the mit integration bee. it contains 5 problems testing various integration techniques like trigonometric substitution and partial fractions.
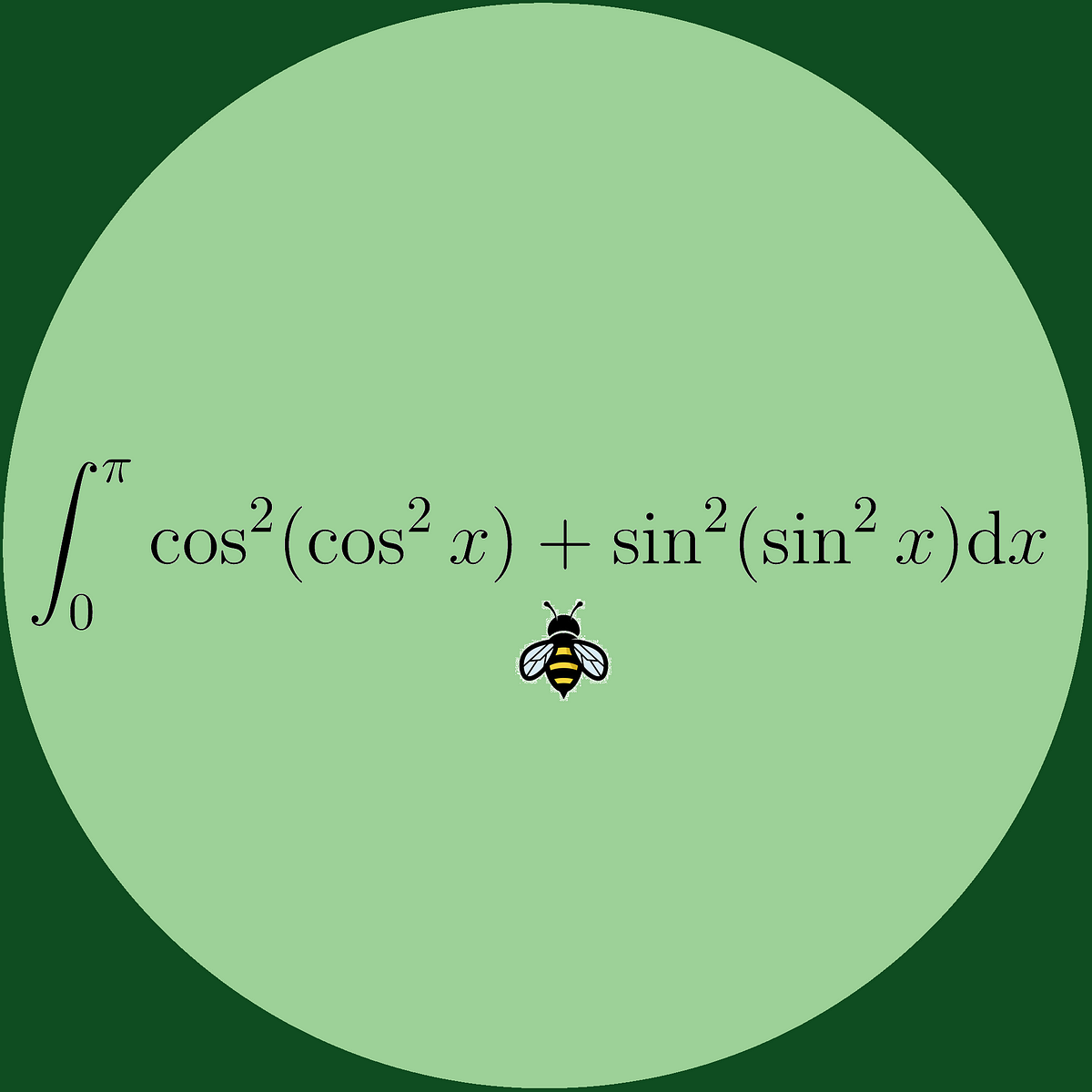
Uk Integration Bee Final 2024 Problem By Wojciech Kowalczyk The integrals and answers can be found at math.mit.edu ~yyao1 pdf 2024 semifinal.pdfplaylist for the full event: playlist?lis. The document describes the problems for the finals of the mit integration bee. it contains 5 problems testing various integration techniques like trigonometric substitution and partial fractions.
Github Pinapueblo Mit Integration Bee 2024 Qualifying Exam Solutions
Comments are closed.