Multivariable Calculus Find The Volume Of A Sphere With Triple

Multivariable Calculus Volumeintegrals Sphere Pdf Multivariable calculus volume of a sphere proof triple integrals. no description has been added to this video. In calculus, two important reductions are used to compute triple integrals. in single variable calculus, one reduces the problem directly to a one dimensional integral by slicing the body along an axes.

Volume As A Triple Integral Multivariable Calculus Studocu Find the volume of the solid that lies within the sphere $x^2 y^2 z^2 =25$, above the $xy$ plane, and outside the cone $z=3\sqrt {x^2 y^2}$. Exercise 2: let e be the region bounded below by the cone z = 3 x 2 3 y 2 and above by the sphere z 2 x 2 y 2 = 4 . set up a triple integral in spherical coordinates to find the volume of the region. In this tutorial, we delve into the application of triple integrals, specifically within the spherical coordinate system, to determine the voluem of sphere from triple integral in speherical coords. Volume of the sphere. in this video, we are going to find the volume of the sphere by using triple integrals in cylindrical coordinates. more.
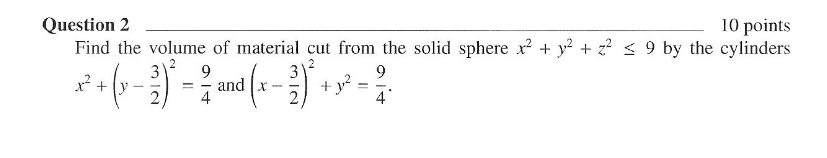
Solved Calculus 3 Triple Integrals Find The Volume Of Chegg In this tutorial, we delve into the application of triple integrals, specifically within the spherical coordinate system, to determine the voluem of sphere from triple integral in speherical coords. Volume of the sphere. in this video, we are going to find the volume of the sphere by using triple integrals in cylindrical coordinates. more. The questions reads: evaluate the iterated integral in spherical coordinates that describes the volume of the solid enclosed by the sphere $x^2 y^2 z^2 = 4a^2$ and the planes $z = 0$ and $z =. The fundamental shapes for integrating in each coordinate system along with the formula are shown in figure 4.3.1. the derivation of the volume formula for the spherical shape is found in section 4.4. The volume of a sphere is the volume of the complement of a cone in that cylinder. cavalieri (1598 1647) would build on archimedes ideas and determine area and volume using tricks now called the cavalieri principle. 1 i'm trying to find the volume of the cap of a sphere with double triple integral. however i keep getting the wrong answer. i have a sphere with a radius of one centered at the orgine and the cap is between z=1 2 and z=1. here's my integral:.

Multivariable Calculus Tutorial Pdf Sphere Volume The questions reads: evaluate the iterated integral in spherical coordinates that describes the volume of the solid enclosed by the sphere $x^2 y^2 z^2 = 4a^2$ and the planes $z = 0$ and $z =. The fundamental shapes for integrating in each coordinate system along with the formula are shown in figure 4.3.1. the derivation of the volume formula for the spherical shape is found in section 4.4. The volume of a sphere is the volume of the complement of a cone in that cylinder. cavalieri (1598 1647) would build on archimedes ideas and determine area and volume using tricks now called the cavalieri principle. 1 i'm trying to find the volume of the cap of a sphere with double triple integral. however i keep getting the wrong answer. i have a sphere with a radius of one centered at the orgine and the cap is between z=1 2 and z=1. here's my integral:.
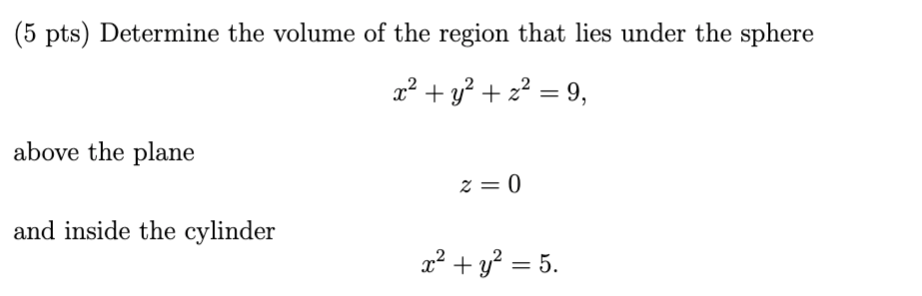
Solved Multivariable Calculus Determine The Volume Of The Chegg The volume of a sphere is the volume of the complement of a cone in that cylinder. cavalieri (1598 1647) would build on archimedes ideas and determine area and volume using tricks now called the cavalieri principle. 1 i'm trying to find the volume of the cap of a sphere with double triple integral. however i keep getting the wrong answer. i have a sphere with a radius of one centered at the orgine and the cap is between z=1 2 and z=1. here's my integral:.
Solved Set Up A Triple Integral To Find The Volume Inside Both The
Comments are closed.