Pdf Matrix Groups And Symmetry

Symmetry Pdf Pdf Symmetry Geometry Groups, especially matrix groups, have now become important in the study of symmetry and have found applications in such disciplines as chemistry and physics. Theorem his ideas lead to the definition of what it is now called a lie group. let g be the symmetry group of a system of differential equations. then the system is solvable by quadrature if and only if g is a solvable group.

Symmetry And Group Theory Pdf Infrared Spectroscopy Group Theory Every symmetry of a given set s is invertible as well, with as inverse another symmetry of s. we now put a first step into the world of abstract algebra, and introduce the notion of a group. In chapter 4 we de ne the idea of a lie group and show that all matrix groups are lie subgroups of general linear groups. in chapter 5 we discuss homeogeneous spaces and show how to recognise them as orbits of smooth actions. In this section we will explore symmetry and the way in which it arises in various contexts with which we are familiar, especially in the geometry of regular polygons (2d) and regular polyhedra (3d), such as the platonic solids. Font type enable dyslexic font downloads expand more download page (pdf) download full book (pdf) resources expand more periodic table physics constants scientific calculator reference expand more.

Color Symmetry And Group Theory Pdf Index Of A Subgroup Group In this section we will explore symmetry and the way in which it arises in various contexts with which we are familiar, especially in the geometry of regular polygons (2d) and regular polyhedra (3d), such as the platonic solids. Font type enable dyslexic font downloads expand more download page (pdf) download full book (pdf) resources expand more periodic table physics constants scientific calculator reference expand more. The tools we introduce allow us to determine the generators for the general linear group, the orthogonal group, the symplectic group, and their special subgroups. Now we will begin discussion of some combinatorial topics that will later aid in our study of representations of the symmetric group. we will discuss young diagrams, young tableaux, and young tabloids, all of which are named after alfred young. Ymmetric group. all elements ar on composit es and tions. we then introduce and define some real world applications followed by mmetric groups. lastly, group structure of symmetric groups and some of the representative theories. 1. symmetry groups in rn ear groups. we write mn or mn(r) for the set of n n matrices over the real numbers. rec ll that an n n matrix a is invertible if there is a matrix b such that ab = i = ba. th we write gln or gln(r) for the set of invertible n n matrices over r. 2 g such that the set g is closed under , in other words a b 2 g whenever a.

Group Theory Part 3 Matrix Algebra Pdf Matrix Mathematics Algebra The tools we introduce allow us to determine the generators for the general linear group, the orthogonal group, the symplectic group, and their special subgroups. Now we will begin discussion of some combinatorial topics that will later aid in our study of representations of the symmetric group. we will discuss young diagrams, young tableaux, and young tabloids, all of which are named after alfred young. Ymmetric group. all elements ar on composit es and tions. we then introduce and define some real world applications followed by mmetric groups. lastly, group structure of symmetric groups and some of the representative theories. 1. symmetry groups in rn ear groups. we write mn or mn(r) for the set of n n matrices over the real numbers. rec ll that an n n matrix a is invertible if there is a matrix b such that ab = i = ba. th we write gln or gln(r) for the set of invertible n n matrices over r. 2 g such that the set g is closed under , in other words a b 2 g whenever a.
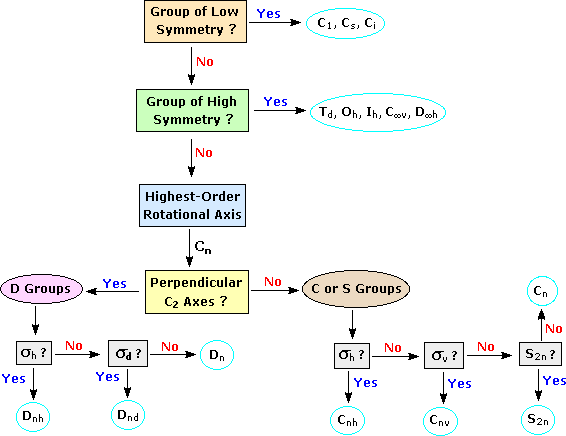
Symmetry And Point Groups Chemistry Libretexts Ymmetric group. all elements ar on composit es and tions. we then introduce and define some real world applications followed by mmetric groups. lastly, group structure of symmetric groups and some of the representative theories. 1. symmetry groups in rn ear groups. we write mn or mn(r) for the set of n n matrices over the real numbers. rec ll that an n n matrix a is invertible if there is a matrix b such that ab = i = ba. th we write gln or gln(r) for the set of invertible n n matrices over r. 2 g such that the set g is closed under , in other words a b 2 g whenever a.
Comments are closed.