Polynomial Functions Of Higher Degree Section 2 2

Polynomial Functions Of Higher Degree Pdf Polynomial Zero Of A Whether the graph of a polynomial function eventually rises or falls can be determined by the function’s degree (even or odd) and by its lead ing coefficient, as indicated in the leading coefficient test. In section 2, we discussed quadratic functions that are of the form 𝑓 (𝑥 ) 𝑎𝑥 2 𝑏𝑥 𝑐, 𝑎 0. a quadratic function is an example of a polynomial function which is written in the form 𝑓 (𝑥 ) 𝑎𝑛 𝑥 𝑛 𝑥 𝑎1 𝑥 𝑎0 where 𝑎𝑛 , , 𝑎1 , 𝑎0 are all real numbers and 𝑛 is a nonnegative integer.

Polynomial Functions Of Higher Degree Section 2 2 If f (x) and d(x) are polynomials such that d(x) 6= 0, and the degree of d(x) is less than or equal to the degree of f (x), then there exist unique polynomials q(x) and r(x) such that. Section 2.2 polynomial functions of higher degree you should know the following basic principles about polynomials. f x anxn. They are smooth curves, with no jumps or sharp points. a polynomial has at most turning points. a polynomial has at most n x intercepts. a polynomial has exactly one y intercept. Study with quizlet and memorize flashcards containing terms like continuous function, leading coefficient test, real zeros of a polynomial function and more.

Section 2 2 Polynomial Functions Of Higher Degree They are smooth curves, with no jumps or sharp points. a polynomial has at most turning points. a polynomial has at most n x intercepts. a polynomial has exactly one y intercept. Study with quizlet and memorize flashcards containing terms like continuous function, leading coefficient test, real zeros of a polynomial function and more. Here are some graphs of polynomial functions: transformations of higher degree polynomial functions. if this is y = x3 if this is y = x4 then what is this?. A polynomial function of degree “n” has at most mins max’s and at most zeros. 2.2 polynomial functions of higher degree we will look at the basic shapes of polynomials and write the end behavior in infinity notation using the leading coefficient test. While we do have (uglier) analogs of the quadratic formula for 3rd and 4th degree polynomial functions, it has actually been proven that there is no such formula for 5th and higher degree polynomial functions.

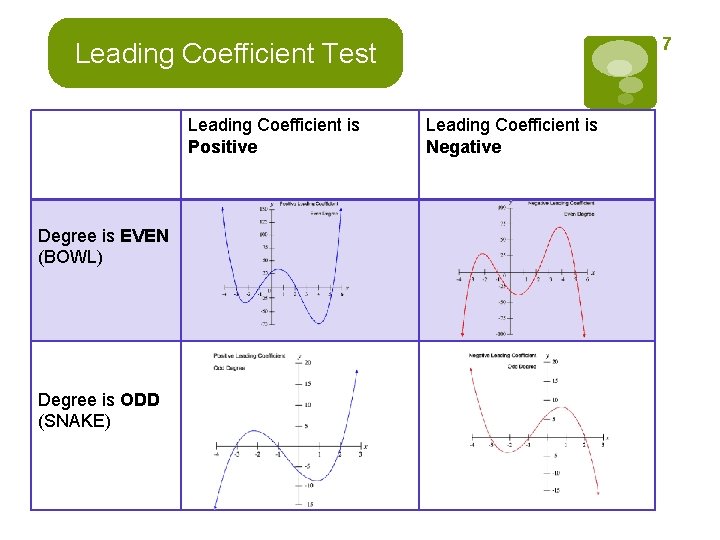
Section 2 2 Polynomial Functions Of Higher Degree Here are some graphs of polynomial functions: transformations of higher degree polynomial functions. if this is y = x3 if this is y = x4 then what is this?. A polynomial function of degree “n” has at most mins max’s and at most zeros. 2.2 polynomial functions of higher degree we will look at the basic shapes of polynomials and write the end behavior in infinity notation using the leading coefficient test. While we do have (uglier) analogs of the quadratic formula for 3rd and 4th degree polynomial functions, it has actually been proven that there is no such formula for 5th and higher degree polynomial functions.