
Probabilités Conditionnelles Formule Des Probabilités Composées Présentation et démonstration de la formule des probabilités composées théorème : soient $a 1,\dots,a m$ des événements tels que $p(a 1\cap\dots\cap a m)\neq 0$. alors : $$p(a 1\cap\dots\cap a m)=p(a 1)p(a 2|a 1)p(a 3|a 1\cap a 2)\cdots p(a m|a 1\cap \dots\cap a {m 1}).$$. En mathématiques, la formule des probabilités composées (ou formule des probabilités conditionnelles en cascade) permet de calculer la probabilité d’une intersection d’ évènements (non nécessairement indépendants) à l’aide de probabilités conditionnelles. soient des évènements dont l’intersection est de probabilité non nulle 1. on a .
120454 Propriété : probabilité d'une intersection ou formule des probabilités composées p(a ∩b) peut se calculer de deux façons : (1) p(a ∩b)=p(a)×pa(b) avec p(a)≠0 (2) p(a ∩b)=p(b)×pb(a) avec p(b)≠0 démonstration : cette propriété se déduit de la définition d'une probabilité conditionnelle. (1) pa(b)= p(b ∩a) p(a). On peut écrire toutes les probabilités comme des probabilités conditionnelles. $p(\omega)=1$. donc pour tout événement $a$ : $p(a)=p \omega(a)$. $p b(b)=1$; $p b(\omega)=1$ ; $p b(\emptyset)=0$. l’événement contraire de « $a$ est réalisé sachant que $b$ est réalisé » est « $\overline{a}$ est réalisé sachant que $b$ est. Énoncer et démontrer la formule des probabilités composées. une urne contient initialement 7 boules noires et 3 boules blanches. on tire successivement 3 boules : si on tire une noire, on l'enlève, si on tire une blanche, on la retire, et on ajoute une noire à la place. quelle est la probabilité de tirer 3 blanches à la suite ?. Le but de cet article est de faire le lien entre les arbres de probabilités et leurs quelques quatre règles et des propriétés très classiques de probabilité: probabilité conditionnelle, formule de bayes, formules des probabilités totales et des probabilités composées.
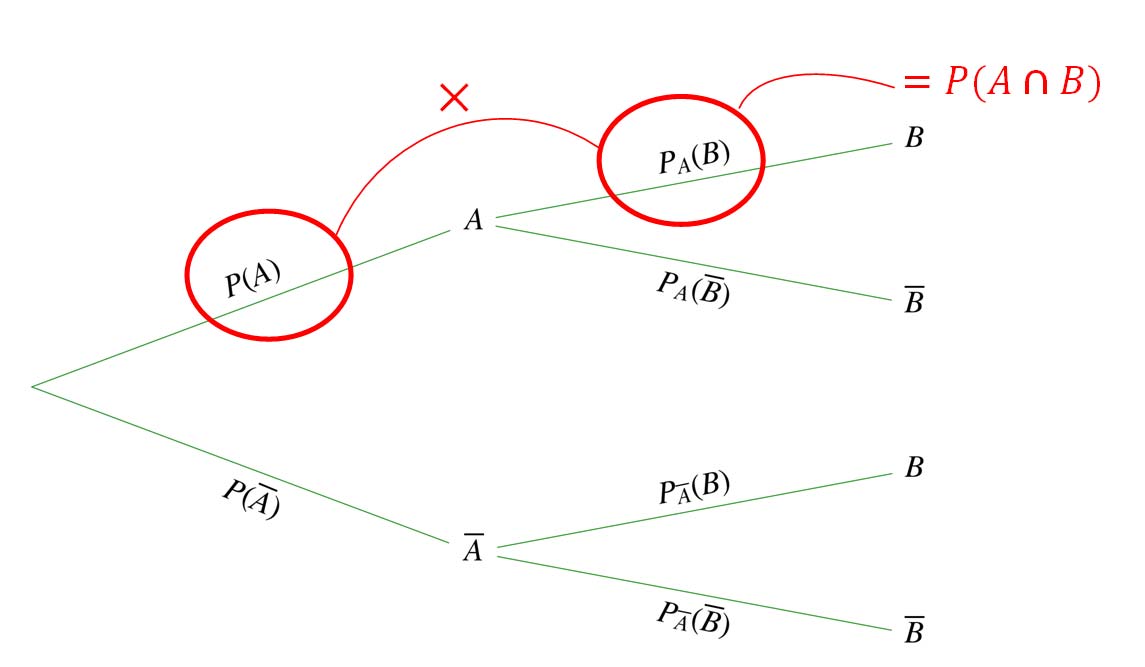
Utiliser La Formule Des Probabilités Conditionnelles Mathématiques Club Énoncer et démontrer la formule des probabilités composées. une urne contient initialement 7 boules noires et 3 boules blanches. on tire successivement 3 boules : si on tire une noire, on l'enlève, si on tire une blanche, on la retire, et on ajoute une noire à la place. quelle est la probabilité de tirer 3 blanches à la suite ?. Le but de cet article est de faire le lien entre les arbres de probabilités et leurs quelques quatre règles et des propriétés très classiques de probabilité: probabilité conditionnelle, formule de bayes, formules des probabilités totales et des probabilités composées. Formule des probabilités composées. Événements indépendants. 1. ce que dit le programme. l’enseignement dispensé en classe de seconde a abordé le modèle probabiliste, dans le cas d’un univers fini. en première, on développe l’étude de ce modèle. l’enseignement s’organise autour des buts suivants :. La formule des probabilités composées peut s'étendre à trois événements a, b et c tels que p(a)≠0 et p(a∩b)≠0 de la façon suivante: $p(a∩b∩c)$ $=p(a)×p(b a)×p(c a∩b)$. Formule de probabilités composées : si \(p(a 1\cap a 2\cap\ldots\cap a n)\neq0\), alors : $${{p\left({\bigcap^n {i=1}a i}\right) }}={{p(a 1)p {a 1}(a 2)\ldots p {a 1\cap a 2\cap\ldots\cap a {n 1} }(a n) }}$$. La probabilité conditionnelle que l’événement b se réalise sachant que l’événement a est réalisé est notée pa(b) et est définie par pa(b) = p(a)p(a∩b). remarque : en réécrivant cette formule on obtient que p(a∩b) = pa(b)×p(a) = pb(a)×p(b). deux événements a et b sont dits indépendants lorsque p(a∩b) = p(a)×p(b).
