Probability Sample Spaces And The Complement Rule 6 1

Ppt 1 Of Chapter 2 Sample Space Probability And Addition Rule Of Probability, sample spaces, and the complement rule (6.1) simple learning pro • 146k views • 5 years ago. Summary tldr this video script introduces the fundamental concepts of probability, focusing on sample spaces and the complement rule. it explains how to calculate the probability of events using favorable outcomes and total outcomes, exemplified by coin flips.
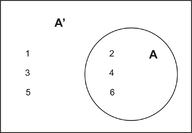
Complement Rule For Probability Read Probability Ck 12 Foundation The reliability of a skin test for active pulmonary tuberculosis (tb) is as follows: of people with tb, 98% have a positive reaction and 2% have a negative reaction; of people free of tb, 99% have a negative reaction and 1% have a positive reaction. To determine the probability on a event occurring, cardano’s idea is to make a list of all the possible outcomes from a random event. for example, a random event might be flipping a coin in which case the set of possible outcomes (the sample space Ω Ω) is given by Ω = {h,t} Ω = {h, t}. To learn how to use special formulas for the probability of an event that is expressed in terms of one or more other events. some events can be naturally expressed in terms of other, sometimes simpler, events. These notes cover the basic de nitions of discrete probability theory, and then present some results including bayes' rule, inclusion exclusion formula, chebyshev's inequality, and the weak law of large numbers.

Complement Rule For Probability Read Probability Ck 12 Foundation To learn how to use special formulas for the probability of an event that is expressed in terms of one or more other events. some events can be naturally expressed in terms of other, sometimes simpler, events. These notes cover the basic de nitions of discrete probability theory, and then present some results including bayes' rule, inclusion exclusion formula, chebyshev's inequality, and the weak law of large numbers. Note: the term sample space reflects the fact that, in statistics, the sible outcomes often consists of the possible samples of a given size, as table 4.2 on page 145. If we roll a standard 6 sided die, describe the sample space and some simple events. the sample space is the set of all possible simple events: {1, 2, 3, 4, 5, 6} some examples of simple events: we roll a 1. we roll a 5. some compound events: we roll a number bigger than 4. we roll an even number. Now that we understand the concept of a sample space, we will define probability. probability: for a sample space s, and an outcome a of s, the following two properties are satisfied. the sum of the probabilities of all the outcomes in s equals 1. The sample space of a random experiment is the collection of all possible outcomes. an event associated with a random experiment is a subset of the sample space.

Complement Rule For Probability Read Probability Ck 12 Foundation Note: the term sample space reflects the fact that, in statistics, the sible outcomes often consists of the possible samples of a given size, as table 4.2 on page 145. If we roll a standard 6 sided die, describe the sample space and some simple events. the sample space is the set of all possible simple events: {1, 2, 3, 4, 5, 6} some examples of simple events: we roll a 1. we roll a 5. some compound events: we roll a number bigger than 4. we roll an even number. Now that we understand the concept of a sample space, we will define probability. probability: for a sample space s, and an outcome a of s, the following two properties are satisfied. the sum of the probabilities of all the outcomes in s equals 1. The sample space of a random experiment is the collection of all possible outcomes. an event associated with a random experiment is a subset of the sample space.

Probability Complement Now that we understand the concept of a sample space, we will define probability. probability: for a sample space s, and an outcome a of s, the following two properties are satisfied. the sum of the probabilities of all the outcomes in s equals 1. The sample space of a random experiment is the collection of all possible outcomes. an event associated with a random experiment is a subset of the sample space.
Complement Probability Definition Meaning
Comments are closed.