
2 6 Geometric Proof Pdf Geometrical proof of a b c whole square formula to derive the expansion of a plus b plus c whole square (a b c)^2 identity in algebraic form. Proving various algebraic identities like (a b)2, (a b)2, (a b c)2, a2 b2, (a b)2, (x a)(x b), (x−a)(x−b), a(b c), (b c)a using geometry.
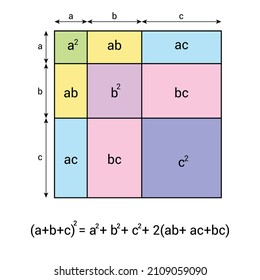
Proof Abc2 Formula Geometric Method Square Stock Vector Royalty Free In this video we are trying to explain algebraic identity (a b c )^2 = a^2 b^2 c^2 2ab 2ac visual explanation usually always stay in our mind. The theorem can be proved algebraically using four copies of a right triangle with sides \(a\), \(b,\) and \(c\) arranged inside a square with side \(c,\) as in the top half of the diagram. the triangles are similar with area \( {\frac {1}{2}ab}\), while the small square has side \(b − a\) and area \((b − a)^2\). The demonstration and proof of heron's formula can be done from elementary consideration of geometry and algebra. i will assume the pythagorean theorem and the area formula for a triangle where b is the length of a base and h is the height to that base. The pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2 proof of the pythagorean theorem using algebra.

Proof Abc2 Formula Geometric Method Square Stock Vector Royalty Free The demonstration and proof of heron's formula can be done from elementary consideration of geometry and algebra. i will assume the pythagorean theorem and the area formula for a triangle where b is the length of a base and h is the height to that base. The pythagorean theorem says that, in a right triangle, the square of a (which is a×a, and is written a 2) plus the square of b (b 2) is equal to the square of c (c 2): a 2 b 2 = c 2 proof of the pythagorean theorem using algebra. Identity i: square of the sum of two terms. ( a b )2 = a2 2ab b2. proof: method i. consider a square with side ( a b ) units. we divide the square into four quadrilaterals – two rectangles with sides ( a and b ) and two squares with sides a and b. In this article i want to demonstrate some heuristics for solving geometric proofs using the methods of vector algebra. an understanding of vector algebra is assumed. my plan is to present three problems solved in full, and to aid the reader in nding the heuristic principles involved. B c d o m∠d m∠b to believe certain geometric principles, it is necessary to have proof. this section intro duces some guidelines for establishing the proof of these geometric properties. several examples are offered to help you develop your own proofs. in the beginning, the form of. In this video i am giving the geometrical proof of (a b c)^3 formula using 3 dimensional figures.click on the below link to watch model of (x a) (x b) (x c)htt.
