43 What Is The Proof That A B 2 A2 2ab B2 Assume that a a and b b are both n × n n × n matrices, how would i prove that (a b)2 =a2 2ab b2 (a b) 2 = a 2 2 a b b 2 for any n × n n × n matrices? you can't, otherwise you'd be proving that 2ab = ab ba 2 a b = a b b a for all square matrices, which isn't true. this is not true. try to find a counterexample. I'm going through cunningham's a logical introduction to proof. an exercise is asking to prove that $a^2 b^2 > 2ab$, by letting $a$ and $b$ be distinct numbers and using the fact $x^2 >0$ i.

A2 B2 Formula Proof And Questions And Answers Thus, (a b) 2 formula is: (a b) 2 = a 2 2ab b 2. to prove the a b whole square formula geometrically, two squares of lengths 'a' and 'b' are attached as shown in the figure below such that two rectangles, each of area ab are formed. we can understand this formula geometrically using the following figure:. Algebraic identity (a b) 2 = a 2 2ab b 2 is verified. the identity (a b) 2 = a 2 2ab b 2 is verified by cutting and pasting of paper. this identity can be verified geometrically by taking other values of a and b. divide a square plot into four parts (quadrilaterals) such that two parts have same area and other two are squares. viva voce. A squared plus b square formula is called the sum of squares formula. it can be expressed as a^2 b^2 = (a b)^2 2ab (or) a^2 b^2 = (a b)^2 2ab. learn how to derive these formulas and see its applications. In this video, geometrical proof of (a b)^2 = a^2 2ab b^2 is explained using a square.
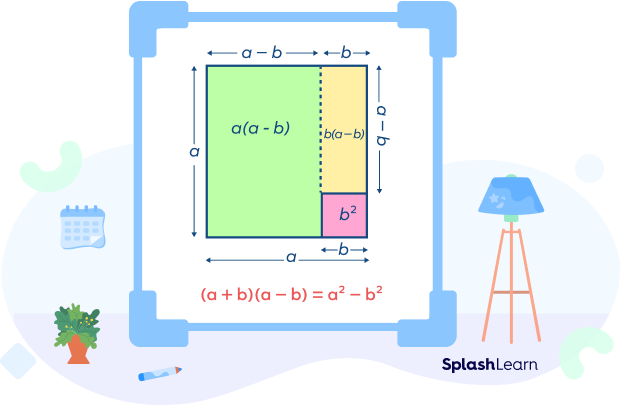
Algebraic Identities Definition Factorization Proof Examples A squared plus b square formula is called the sum of squares formula. it can be expressed as a^2 b^2 = (a b)^2 2ab (or) a^2 b^2 = (a b)^2 2ab. learn how to derive these formulas and see its applications. In this video, geometrical proof of (a b)^2 = a^2 2ab b^2 is explained using a square. No, the formula (a b) 2 = a 2 2ab b 2 is a property of numbers called the binomial expansion, and it does not apply to matrices. in general, matrix operations such as addition and multiplication have different rules and properties than those of numbers. $\begingroup$ a combinatorial proof is usually understood as one that establishes equality by counting the same group of things in two different ways. here the whole square is $(a b)^2$ and the four regions are $a^2,b^2,ab,ab$ $\endgroup$. Actually the visual proof conveys that fairly well the diagram really shows a 2 ab ba b 2, and it's up to the viewer to apply commutativity of multiplication to simplify. of course, until you invent a rectangle that changes shape when rotated through 90 degrees, ab and ba will still be the same size :). Applying the square to brackets works only when you multiply, not when you add. e.g. (a*b)^ (2) = a^2 * b^2 is true. this is because (a*b)^ (2) = (a*b)* (a*b) = a*a * b*b. however if you add then it doesn't work: (a b)^2 = (a b) * (a b). think about it now, if you have a b lots of a b, then you have a lots of a b plus b lots of a b.
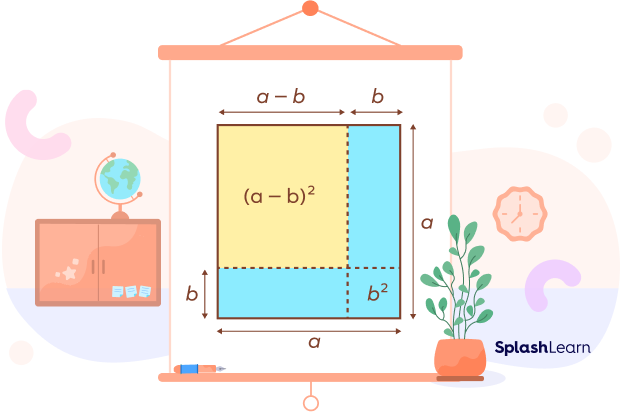
Algebraic Identities Definition Factorization Proof Examples No, the formula (a b) 2 = a 2 2ab b 2 is a property of numbers called the binomial expansion, and it does not apply to matrices. in general, matrix operations such as addition and multiplication have different rules and properties than those of numbers. $\begingroup$ a combinatorial proof is usually understood as one that establishes equality by counting the same group of things in two different ways. here the whole square is $(a b)^2$ and the four regions are $a^2,b^2,ab,ab$ $\endgroup$. Actually the visual proof conveys that fairly well the diagram really shows a 2 ab ba b 2, and it's up to the viewer to apply commutativity of multiplication to simplify. of course, until you invent a rectangle that changes shape when rotated through 90 degrees, ab and ba will still be the same size :). Applying the square to brackets works only when you multiply, not when you add. e.g. (a*b)^ (2) = a^2 * b^2 is true. this is because (a*b)^ (2) = (a*b)* (a*b) = a*a * b*b. however if you add then it doesn't work: (a b)^2 = (a b) * (a b). think about it now, if you have a b lots of a b, then you have a lots of a b plus b lots of a b.
