Proof Of Power Rule Of Derivatives

Power Rule How To W 9 Step By Step Examples In this section we prove several of the rules formulas properties of derivatives that we saw in derivatives chapter. Now we know the formula for the power rule derivative, let us now prove the formula using different methods. we will prove the general formula for the power rule using the principle of mathematical induction and the binomial theorem.
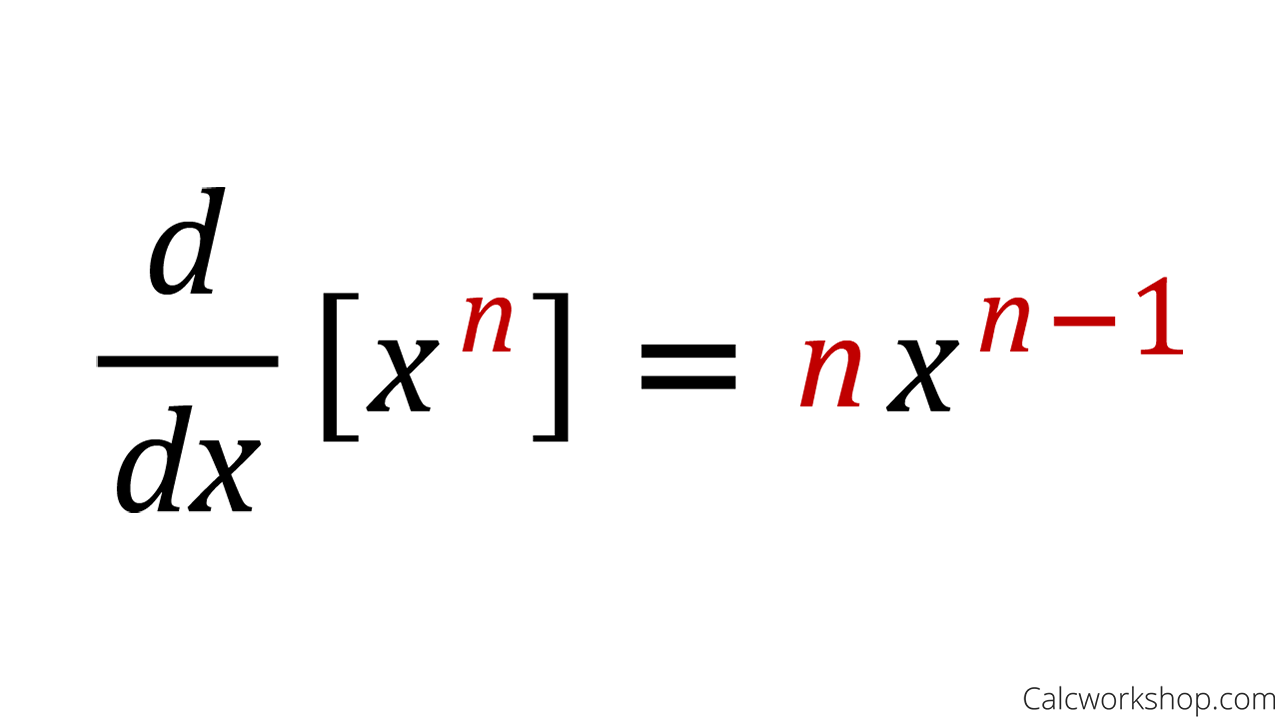
Power Rule How To W 9 Step By Step Examples The power rule for differentiation was derived by isaac newton and gottfried wilhelm leibniz, each independently, for rational power functions in the mid 17th century, who both then used it to derive the power rule for integrals as the inverse operation. Step 1: proof of the power rule for non negative integer exponents. in this step, we assume that $f (x) = x^n,$ where $n$ is some positive integer: $0, 1, 2, 3,$ . first, if $n$ happens to be zero, $f (x) = x^0 = 1,$ a constant, and so its derivative is zero, by the result we proved in the text. thus, assume that $n$ is a positive integer. Proof: suppose $$y = x^ {\frac {p} {q}}$$ raising both sides to the $q$ power, we get an equation involving integer powers of $x$ and $y$ $$y^q = x^p$$ as such, we can differentiate both sides using the power rule for derivatives (for integer powers) to obtain $$qy^ {q 1} \frac {dy} {dx} = px^ {p 1}$$. Learn how to derive power rule of differentiation to prove derivative of x^n is equal to nx^ (n 1) in differential calculus from first principle.
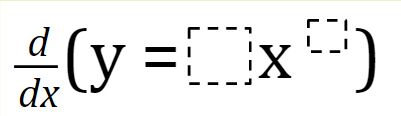
Derivatives Power Rule Open Middle Proof: suppose $$y = x^ {\frac {p} {q}}$$ raising both sides to the $q$ power, we get an equation involving integer powers of $x$ and $y$ $$y^q = x^p$$ as such, we can differentiate both sides using the power rule for derivatives (for integer powers) to obtain $$qy^ {q 1} \frac {dy} {dx} = px^ {p 1}$$. Learn how to derive power rule of differentiation to prove derivative of x^n is equal to nx^ (n 1) in differential calculus from first principle. Learn the proof of the power rule of derivatives. the proof involves newton's quotient and the binomial theorem. enjoy! more. In calculus, the power rule is the following rule of differentiation. using the rules of differentiation and the power rule, we can calculate the derivative of polynomials as follows:. Power rule proof this article will walk you through how to prove the power rule and take the derivative of any polynomial. we are going to prove every step of the way. The power rule d what is the derivative of x r? we answered this question first for positive dx integer values of r, for all integers, and then for rational values of r: d xr = r−1 rx dx we’ll now prove that this is true for any real number r. we can do this two ways:.

Lesson Power Rule Of Derivatives Nagwa Worksheets Library Learn the proof of the power rule of derivatives. the proof involves newton's quotient and the binomial theorem. enjoy! more. In calculus, the power rule is the following rule of differentiation. using the rules of differentiation and the power rule, we can calculate the derivative of polynomials as follows:. Power rule proof this article will walk you through how to prove the power rule and take the derivative of any polynomial. we are going to prove every step of the way. The power rule d what is the derivative of x r? we answered this question first for positive dx integer values of r, for all integers, and then for rational values of r: d xr = r−1 rx dx we’ll now prove that this is true for any real number r. we can do this two ways:.
Comments are closed.