Prove That Determinant B C 2a2 A2 B2 C A 2 B2 2abc A B C 3 C2 C2 A

Prove That Determinant B C 2a2 A2 B2 C A 2 B2 2abc A B C 3 C2 C2 A Alternatively, it is easily seen that the determinant of the given matrix is a homogeneous polynomial $p(a,b,c)$ in $a$, $b$, and $c$ of degree $5$. furthermore, $p(a,b,c)=0$ if any two of the three inputs are equal. Question 8 by using properties of determinants, show that: (ii) | 8(1&1&1@a&b&c@a3&b3&c3)| = (a – b) (b – c) (c – a) (a b c) solving l.h.s | 8(1&1&1@a&b&c@a3&b3&c3)| applying c1 → c1 − c2 = | 8(𝟏−𝟏&1&1@a−b&b&c@𝐚𝟑 −𝐛𝟑&b3 &c3)| = | 8(𝟎&1&1@a−b&b&c@(𝐚 −𝐛)(𝐚𝟐 𝐛𝟐 𝐚𝐛) &b3&c3)| = | 8.

Prove Using Properties Of Determinants A B C 2a 2a 2b B C A 2a 2c Misc 6 prove that | 8(a2&bc&ac c2@a2 ab&b2&ac@ab&b2 bc&c2)| = 4a2b2c2 solving l.h.s | 8(a2&bc&ac c2@a2 ab&b2&ac@ab&b2 bc&c2)| = | 8(𝐚(𝑎)&𝐛(c)&𝐜(a c)@𝐚(𝑎 𝑏)&𝐛(b)&𝐜(a)@𝐚(𝑏)&𝐛(b c)&𝐜(c))| taking out a common from c1 ,b common from c2 & c common from c3 = abc | 8(a&c&a c@𝑎 𝑏&b&a@𝑏&b c&c). Using properties of determinants, prove the following: | (a 2,a 2 (b c) 2, bc) (b 2,b 2 (c a) 2,ca) (c 2,c 2 (a b) 2,ab)| = (a b) (b c) (c a) (a b c) (a 2 b 2 c 2) challenge your friends with exciting quiz games – click to play now!. Using properties of determinants prove that: |((b c)^2 a^2 bc) ((c a)^2 b^2,ca) ((a b)^2, c^2, ab)| = (a^2 b^2 c^2) (a b) (b c) (c a) (a b c) asked aug 3, 2021 in determinants by kumararun ( 15.9k points). Using properties of determinants, calculate the determinan : a=[(1,a1,0,b1,0),(0,a2,0,b2,0),(0,a3,1,b3,0),(0,a4,0,b4,0),(0,a5,0,b5,1)].

Without Expanding The Determinant Prove That A A 2 Bc B B 2 Ca Using properties of determinants prove that: |((b c)^2 a^2 bc) ((c a)^2 b^2,ca) ((a b)^2, c^2, ab)| = (a^2 b^2 c^2) (a b) (b c) (c a) (a b c) asked aug 3, 2021 in determinants by kumararun ( 15.9k points). Using properties of determinants, calculate the determinan : a=[(1,a1,0,b1,0),(0,a2,0,b2,0),(0,a3,1,b3,0),(0,a4,0,b4,0),(0,a5,0,b5,1)]. Use $$c 1'=c 1 c 3$$ and $$c 2'=c 2 c 3$$ where $c r$ is the $r$th column, $c r'$ is the resultant $r$th column see also: factorise the determinant $\det\bigl(\begin{smallmatrix} a^3 a^2 & a & 1 \\ b^3 b^2 & b & 1 \\ c^3 c^2 & c &1\end{smallmatrix}\bigr)$. Using properties of determinant prove that: |[b c, c a, a b],[c a, a b, b c],[a b, b c, c a]|=2(a b c)(ab bc ca a^2 b^2 c^2) `. Using properties of determinants, prove the following: `|(a, b,c),(a b, b c, c a),(b c, c a, a b)| = a^3 b^3 c^3 3abc`. solve for x : `|("a" "x","a" "x","a" "x"),("a" "x","a" "x","a" "x"),("a" "x","a" "x","a" "x")| = 0`, using properties of determinants. without expanding determinants, show that. Question 8 by using properties of determinants, show that: (i) | 8(1&𝑎&𝑎2@1&𝑏&𝑏2@1&𝑐&𝑐2)| = (a b) (b c)(c – a) solving l.h.s | 8(1&𝑎&𝑎2@1&𝑏&𝑏2@1&𝑐&𝑐2)| applying r1 → r1 − r2 = | 8(𝟏−𝟏&𝑎−𝑏&𝑎^2−𝑏^2@1&𝑏&𝑏2@1&𝑐&𝑐2 ) | = | 8(𝟎&(𝑎−𝑏)&(𝑎−𝑏)(𝑎 𝑏.

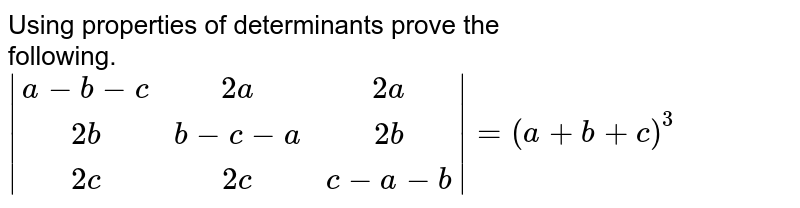
Using Properties Of Determinants Prove The Following A B C A B Use $$c 1'=c 1 c 3$$ and $$c 2'=c 2 c 3$$ where $c r$ is the $r$th column, $c r'$ is the resultant $r$th column see also: factorise the determinant $\det\bigl(\begin{smallmatrix} a^3 a^2 & a & 1 \\ b^3 b^2 & b & 1 \\ c^3 c^2 & c &1\end{smallmatrix}\bigr)$. Using properties of determinant prove that: |[b c, c a, a b],[c a, a b, b c],[a b, b c, c a]|=2(a b c)(ab bc ca a^2 b^2 c^2) `. Using properties of determinants, prove the following: `|(a, b,c),(a b, b c, c a),(b c, c a, a b)| = a^3 b^3 c^3 3abc`. solve for x : `|("a" "x","a" "x","a" "x"),("a" "x","a" "x","a" "x"),("a" "x","a" "x","a" "x")| = 0`, using properties of determinants. without expanding determinants, show that. Question 8 by using properties of determinants, show that: (i) | 8(1&𝑎&𝑎2@1&𝑏&𝑏2@1&𝑐&𝑐2)| = (a b) (b c)(c – a) solving l.h.s | 8(1&𝑎&𝑎2@1&𝑏&𝑏2@1&𝑐&𝑐2)| applying r1 → r1 − r2 = | 8(𝟏−𝟏&𝑎−𝑏&𝑎^2−𝑏^2@1&𝑏&𝑏2@1&𝑐&𝑐2 ) | = | 8(𝟎&(𝑎−𝑏)&(𝑎−𝑏)(𝑎 𝑏.

Prove That A B C 2a 2a 2b B C A 2b 2c 2c C A B Using properties of determinants, prove the following: `|(a, b,c),(a b, b c, c a),(b c, c a, a b)| = a^3 b^3 c^3 3abc`. solve for x : `|("a" "x","a" "x","a" "x"),("a" "x","a" "x","a" "x"),("a" "x","a" "x","a" "x")| = 0`, using properties of determinants. without expanding determinants, show that. Question 8 by using properties of determinants, show that: (i) | 8(1&𝑎&𝑎2@1&𝑏&𝑏2@1&𝑐&𝑐2)| = (a b) (b c)(c – a) solving l.h.s | 8(1&𝑎&𝑎2@1&𝑏&𝑏2@1&𝑐&𝑐2)| applying r1 → r1 − r2 = | 8(𝟏−𝟏&𝑎−𝑏&𝑎^2−𝑏^2@1&𝑏&𝑏2@1&𝑐&𝑐2 ) | = | 8(𝟎&(𝑎−𝑏)&(𝑎−𝑏)(𝑎 𝑏.