Prove That The Roots Of The Equation 2kx25x K0 Are Real And Distinct For All Real Values Of K

Solved 9 Prove That The Roots Of The Equation 2kx2 5x K 0 Chegg Prove that the roots of the equation 2kx^2 5x k=0 are real and distinct for all values of k. Find the set of values of the constant k for which the line y = 2 x k meets the curve y = 1 2 k x x 2 at two distinct points.

Solved The Quadratic Equation K 1 X 2 2x 2k 3 0 Where K Has To prove that the roots of the quadratic equation 2kx^ {2} 5x k = 0 2kx2 5x−k=0 are real and distinct for all real values of k k, we can use the discriminant method. Adding 25 to both sides, we get: \ [25 8k^2 \geq 25\] thus, the discriminant is always greater than or equal to 25, which means it is always positive. therefore, the roots of the equation \ (2kx^2 5x k = 0\) are real and distinct for all values of \ (k\). In this case, \ ( \delta = 25 8k^2 \) is always positive, confirming the roots' nature for all real \ ( k \). this method is crucial in algebra for analyzing the properties of quadratic equations. The discriminant is b 2 4ac, and for the roots to be real, it must be at least 0. in this problem, a=k, b=5, and c= 2k. hence, the discriminant is 5 2 4 (k) ( 2k) = 25 8k 2 which is positive for all real k.

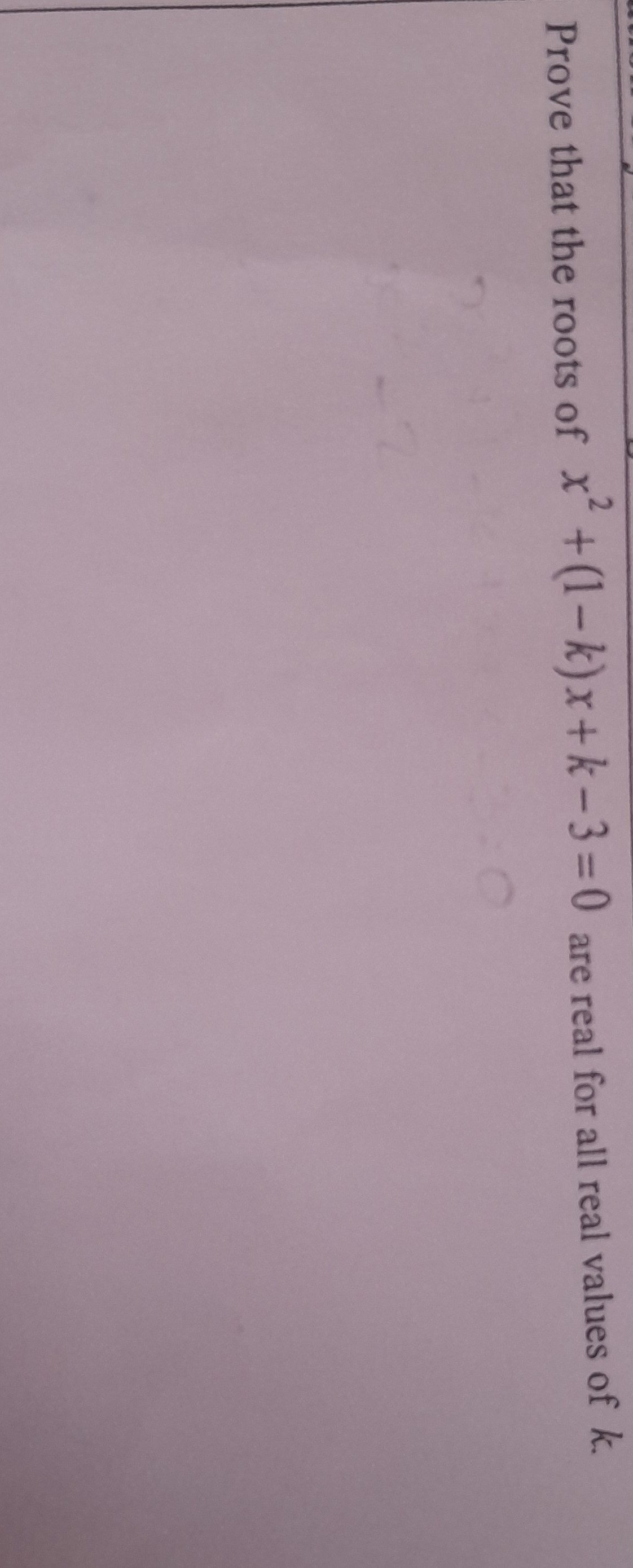
Prove That The Roots Of X 2 1 K X K 3 0 Are Real For All Real Values In this case, \ ( \delta = 25 8k^2 \) is always positive, confirming the roots' nature for all real \ ( k \). this method is crucial in algebra for analyzing the properties of quadratic equations. The discriminant is b 2 4ac, and for the roots to be real, it must be at least 0. in this problem, a=k, b=5, and c= 2k. hence, the discriminant is 5 2 4 (k) ( 2k) = 25 8k 2 which is positive for all real k. Find the largest value of k such that the roots of the equation 2x^2 5x k=0 are real. Answer to prove that the roots of the equation 2kx 2 5x k 0 are real and distinct for all real values of k we need to show that the discriminant of the quadratic equation is always positive which means that the equation has two distinct real roots the discriminant of a quadratic equation ax 2 bx c 0 is given by b 2 4ac so the discriminant of. Step by step explanation: the discriminant is b2 4ac, and for the roots to be real, it must be at least 0. in this problem, a=k, b=5, and c= 2k. hence, the discriminant is 52 4 (k) ( 2k) = 25 8k2 which is positive for all real k. To prove that the roots of the equation k 2 x 2k = 0 are real and distinct for all real values of k, we can use the concept of the discriminant from quadratic equations. the discriminant d can be analyzed further: since (k 2)2 is a square of a binomial, it is always ≥ 0 for all real values of k.