
The Sum And The Product Of Roots Of Quadratic Equations Pdf Finding the sum and product of the roots of a cubic equations: an equation in which at least one term is raised to the power of 3 but no term is raised to any higher power is called a cubic equation. the general form of a cubic equation is ax 3 bx 2 cx d = 0 where a, b, c and d are constants. Quadratic equation: sum and product of roots: the solutions or the roots of the above quadratic equation can be given by quadratic formula as : and is denoted by d or Δ. the relationship is given as: sum of roots. the product of roots is given by ratio of the constant term and the coefficient of. let us try to prove this graphically.

Sum And Product Of Quadratic Equation Roots With Examples Formula for sum and products of roots of quadratic equation with several examples, practice problems and diagrams. For a cubic equation of the form \(ax^3 bx^2\) the sum of the roots is equal to the opposite of the coefficient of the quadratic term divided by the coefficient of the cubic term: \(\frac{ b}{a}\). the product of the roots is equal to the constant term divided by the coefficient of the cubic term: \(\frac{d}{a}\). Example: what is an equation whose roots are 5 √2 and 5 − √2. the sum of the roots is (5 √2) (5 − √2) = 10 the product of the roots is (5 √2) (5 − √2) = 25 − 2 = 23. and we want an equation like: ax 2 bx c = 0. We see where the sum and product of the roots of quadratic equations (alpha and beta) can be used to solve problems.
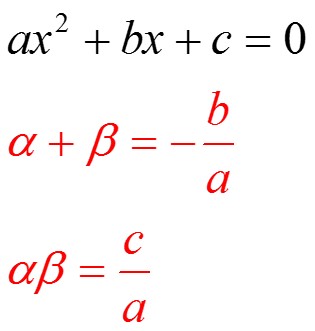
Sum And Product Of Roots Of A Quadratic Equation Mathexams Example: what is an equation whose roots are 5 √2 and 5 − √2. the sum of the roots is (5 √2) (5 − √2) = 10 the product of the roots is (5 √2) (5 − √2) = 25 − 2 = 23. and we want an equation like: ax 2 bx c = 0. We see where the sum and product of the roots of quadratic equations (alpha and beta) can be used to solve problems. Use the sum and product of roots formulas to answer the questions below: 2 kx k 1 0 are and 2 . find the value(s) of k. b) the roots of the quadratic equation x2 6x c are k and k – 1. find the value of c. c) the roots of the quadratic equation 2x2 9x k are m 2 and m – 3. find the value of k. For the quadratic equation a x2 bx c = 0 , let the roots be alpha ( α ) and beta ( β ). therefore: find the simplest quadratic equation with the roots 2 and 3. the simplest cubic has 1 as the coefficient of x3 . sum of roots = 5 (change the sign) product of roots = 6 (don’t change the sign) so simplest equation is x2 − 5x 6 = 0 . The sum of the roots of a quadratic equation is equal to the negation of the coefficient of the second term, divided by the leading coefficient. the product of the roots of a quadratic equation is equal to the constant term (the third term), divided by the leading coefficient. If a quadratic equation is given in standard form, we can find the sum and product of the roots using coefficient of x 2, x and constant term. let us consider the standard form of a quadratic equation, ax 2 bx c = 0 (here a, b and c are real and rational numbers) let α and β be the two zeros of the above quadratic equation.

Sum And Product Of Roots Of Quadratic Equation By Mathamaniacs Tpt Use the sum and product of roots formulas to answer the questions below: 2 kx k 1 0 are and 2 . find the value(s) of k. b) the roots of the quadratic equation x2 6x c are k and k – 1. find the value of c. c) the roots of the quadratic equation 2x2 9x k are m 2 and m – 3. find the value of k. For the quadratic equation a x2 bx c = 0 , let the roots be alpha ( α ) and beta ( β ). therefore: find the simplest quadratic equation with the roots 2 and 3. the simplest cubic has 1 as the coefficient of x3 . sum of roots = 5 (change the sign) product of roots = 6 (don’t change the sign) so simplest equation is x2 − 5x 6 = 0 . The sum of the roots of a quadratic equation is equal to the negation of the coefficient of the second term, divided by the leading coefficient. the product of the roots of a quadratic equation is equal to the constant term (the third term), divided by the leading coefficient. If a quadratic equation is given in standard form, we can find the sum and product of the roots using coefficient of x 2, x and constant term. let us consider the standard form of a quadratic equation, ax 2 bx c = 0 (here a, b and c are real and rational numbers) let α and β be the two zeros of the above quadratic equation.
