Reciprocal Functions Basic Introduction

Characteristics And Properties Of Reciprocal Functions Understanding This algebra video tutorial provides a basic introduction into reciprocal functions. it explains how to graph them using the vertical and horizontal asympto. Reciprocal functions consist of two components: a constant on the numerator and an algebraic expression in the denominator. from its definition to its graph, we’ll learn extensively about reciprocal functions in this article.

Reciprocal Function Pdf Function Mathematics Complex Number A concise guide to reciprocal functions with graphing tips, transformation rules, asymptote insights, and example problems. The reciprocal function is a mathematical function that calculates the reciprocal, or multiplicative inverse, of a given number. it is defined as f (x) = 1 x, where x is the input value and f (x) is the output value. Definition a reciprocal function is a function of the form $f (x) = \frac {1} {g (x)}$, where $g (x)$ is a non zero polynomial. the simplest example is $f (x) = \frac {1} {x}$. Q: what is the standard equation for a reciprocal function? the standard equation for a reciprocal function is y = a (x h) k, where a, h, and k are variables that determine various characteristics of the graph.
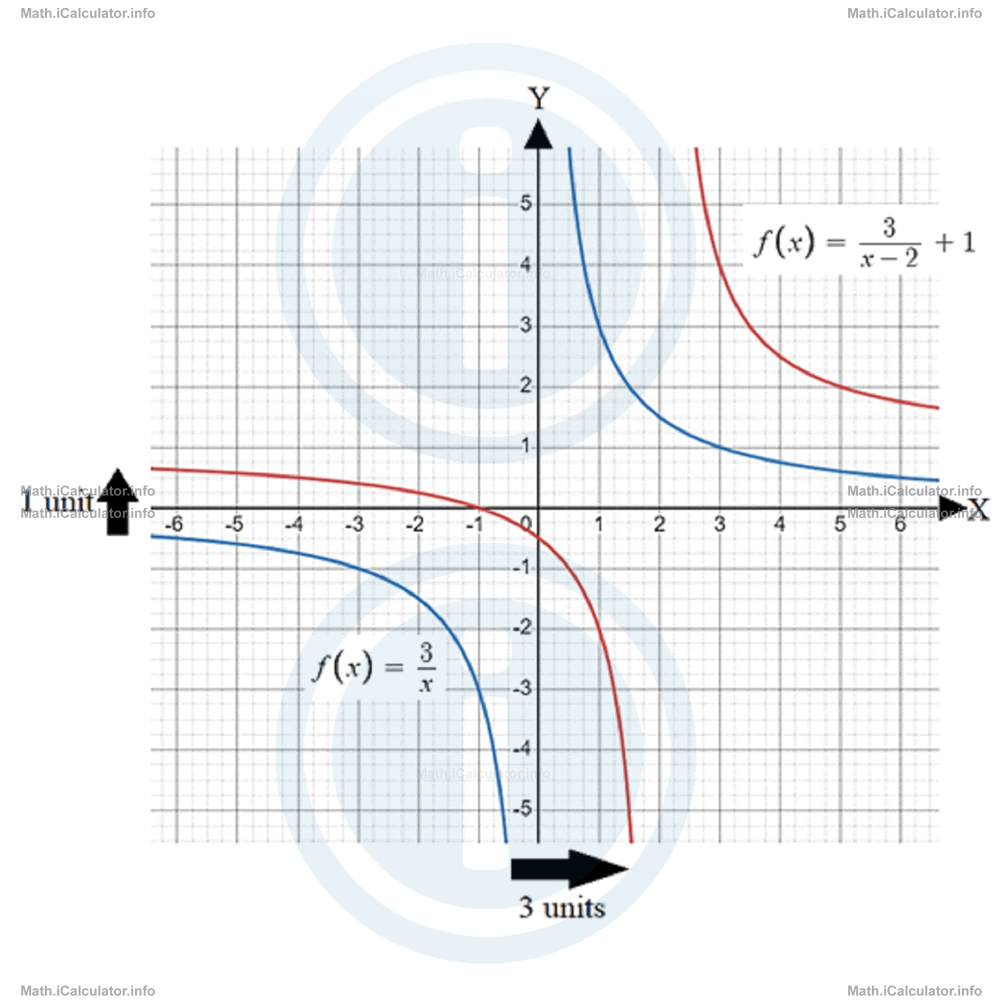
Reciprocal Function Icalculator邃 Definition a reciprocal function is a function of the form $f (x) = \frac {1} {g (x)}$, where $g (x)$ is a non zero polynomial. the simplest example is $f (x) = \frac {1} {x}$. Q: what is the standard equation for a reciprocal function? the standard equation for a reciprocal function is y = a (x h) k, where a, h, and k are variables that determine various characteristics of the graph. Reciprocal functions are used in various fields such as physics, engineering, and economics. for example, in physics, the relationship between the period and frequency of a wave is reciprocal. in economics, the concept of elasticity often involves reciprocal relationships. In this beginner friendly lesson, we introduce one of the most important non linear functions in advanced math: the reciprocal function. learn what reciprocal functions look like, how. Introduction do you remember when you first learned what the reciprocal of a fraction was in elementary school? in this lesson you will learn about reciprocal functions. Indicate clearly in each graph any asymptotes and the coordinates of any intersections with the coordinate axes. y = − , x ≠ 0 . y = 2 − , x ≠ 0 . indicate clearly the coordinates of any points of intersection between coordinate axes. state the equations of the two asymptotes of c .

Online Tutoring Math English Science Tutoring Sat Psat Gmat Reciprocal functions are used in various fields such as physics, engineering, and economics. for example, in physics, the relationship between the period and frequency of a wave is reciprocal. in economics, the concept of elasticity often involves reciprocal relationships. In this beginner friendly lesson, we introduce one of the most important non linear functions in advanced math: the reciprocal function. learn what reciprocal functions look like, how. Introduction do you remember when you first learned what the reciprocal of a fraction was in elementary school? in this lesson you will learn about reciprocal functions. Indicate clearly in each graph any asymptotes and the coordinates of any intersections with the coordinate axes. y = − , x ≠ 0 . y = 2 − , x ≠ 0 . indicate clearly the coordinates of any points of intersection between coordinate axes. state the equations of the two asymptotes of c .
Comments are closed.