Reduction Formulas For Integration 42 Off In integral calculus, integration by reduction formulae is a method relying on recurrence relations. it is used when an expression containing an integer parameter, usually in the form of powers of elementary functions, or products of transcendental functions and polynomials of arbitrary degree, can't be integrated directly. Reduction formulas in integration are given here with example questions. click now to learn the formula of reduction for trigonometric, inverse trigonometric, hyperbolic, exponential, log and algebraic functions.
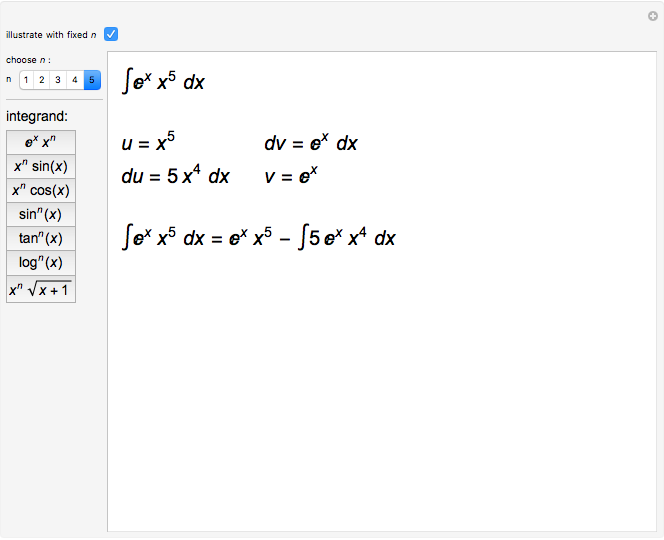
Reduction Formulas For Integrals Wolfram Demonstrations Project Learn how to use reduction formulas to simplify integrals that depend on some integer n. see examples, theorems and applications of reduction formulas for trigonometric functions. Reduction formula is helpful to find the integration of higher order expressions, in a simple and less number of steps. understand the reduction formula with examples and faqs. Integration of higher order terms consisting of logarithmic, algebraic, and trigonometric functions are simplified by reduction formulas. in the reduction formula, higher order degree terms are given a degree n. reduction formulas with degree n are derived from the integration base formulas. When using a reduction formula to solve an integration problem, we apply some rule to rewrite the integral in terms of another integral which is a little bit simpler. we may have to rewrite that integral in terms of another integral, and so on for n steps, but we eventually reach an answer.
Solution Integration Simple Reduction Formulas Studypool Integration of higher order terms consisting of logarithmic, algebraic, and trigonometric functions are simplified by reduction formulas. in the reduction formula, higher order degree terms are given a degree n. reduction formulas with degree n are derived from the integration base formulas. When using a reduction formula to solve an integration problem, we apply some rule to rewrite the integral in terms of another integral which is a little bit simpler. we may have to rewrite that integral in terms of another integral, and so on for n steps, but we eventually reach an answer. Obtain the reduction formula for β«π π π π π π . ππ. π₯π₯ πππππ π . ππ. π₯π₯ π₯π₯π₯π₯. solution: let i. m,n = β«π π π π π π . ππ. π₯π₯ πππππ π . ππ. π₯π₯ π₯π₯π₯π₯. ππ= β«π π π π π π π₯π₯. Integration by reduction formulas enable us to solve complex integration problems. it can be used for trigonometric functions, power of elementary functions, product of two or more complex functions etc. Reduction formulas. sometimes we may be interested in deriving a reduction formula for an integral, or a general identity for a seemingly complex integral. the list below outlines the most common reduction formulas: reduction formula for sine: $\int \sin ^n x \: dx = \frac{1}{n} \cos x \sin ^{n 1} x \frac{n 1}{n} \int \sin ^{n 2} x \: dx$. Reduction formulas tend to calculate the solution of integral complex problems and help us to reduce the integral degree and evaluate the integrals in a limited number of steps. the different types of reduction formulas are: reduction formula for exponential functions; reduction formula for inverse trigonometric functions.
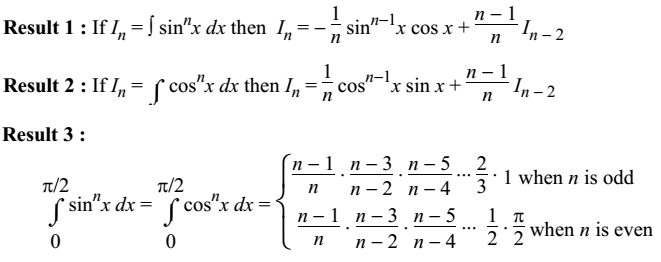
Reduction Formulae For Integration Study Page Obtain the reduction formula for β«π π π π π π . ππ. π₯π₯ πππππ π . ππ. π₯π₯ π₯π₯π₯π₯. solution: let i. m,n = β«π π π π π π . ππ. π₯π₯ πππππ π . ππ. π₯π₯ π₯π₯π₯π₯. ππ= β«π π π π π π π₯π₯. Integration by reduction formulas enable us to solve complex integration problems. it can be used for trigonometric functions, power of elementary functions, product of two or more complex functions etc. Reduction formulas. sometimes we may be interested in deriving a reduction formula for an integral, or a general identity for a seemingly complex integral. the list below outlines the most common reduction formulas: reduction formula for sine: $\int \sin ^n x \: dx = \frac{1}{n} \cos x \sin ^{n 1} x \frac{n 1}{n} \int \sin ^{n 2} x \: dx$. Reduction formulas tend to calculate the solution of integral complex problems and help us to reduce the integral degree and evaluate the integrals in a limited number of steps. the different types of reduction formulas are: reduction formula for exponential functions; reduction formula for inverse trigonometric functions.