
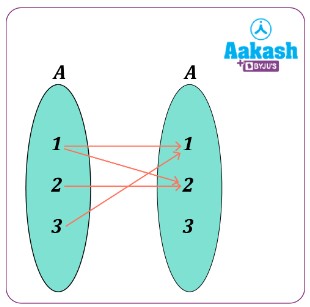
Reflexive Symmetric Transitive Equivalence Number Of Relations Aesl Let us define relation r on set a = {1, 2, 3} we will check reflexive, symmetric and transitive r = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} check reflexive if the relation is reflexive, then (a, a) ∈ r for every a ∈ {1,2,3} since (1, 1) ∈ r ,(2, 2) ∈ r & (3, 3) ∈ r ∴ r is reflexive check symmetric. It is easy to check that \(s\) is reflexive, symmetric, and transitive. let \({\cal l}\) be the set of all the (straight) lines on a plane. define a relation \(p\) on \({\cal l}\) according to \((l 1,l 2)\in p\) if and only if \(l 1\) and \(l 2\) are parallel lines.
Reflexive Symmetric Transitive Equivalence Number Of Relations Aesl To prove a relation to be equivalence, we have to prove the conditions of all three i.e. reflexive, symmetric and transitive relation. reflexive: let x ,then x x=0 is an integer. therefore, x r x ∀ x ∈ r ; symmetric: let x,y such that x r y. then x y is an integer. thus, y – x = – ( x – y), is also an integer. therefore y r x. Equivalence relation is a type of relation that satisfies three fundamental properties: reflexivity, symmetry, and transitivity. these properties ensure that it defines a partition on a set, where elements are grouped into equivalence classes based on their similarity or equality. • definition: let r be a binary relation on a. • r is reflexive if for all x ∈ a, ( x,x ) ∈ r. (equivalently, for all x e a, x r x.) • r is symmetric if for all x,y ∈ a, ( x,y ) ∈ r implies ( y,x ) ∈ r. (equivalently, for all x,y ∈ a, x r y implies that y r x.). A relation that is reflexive, symmetric and transitive is an equivalence relation. in example 8.2.8 we proved that the relation given by (m, n) ∈ r ⇔ 3 ∣ (m − n) is an equivalence relation since we proved it is reflexive, symmetric, and transitive.
Reflexive Symmetric Transitive Equivalence Number Of Relations Aesl • definition: let r be a binary relation on a. • r is reflexive if for all x ∈ a, ( x,x ) ∈ r. (equivalently, for all x e a, x r x.) • r is symmetric if for all x,y ∈ a, ( x,y ) ∈ r implies ( y,x ) ∈ r. (equivalently, for all x,y ∈ a, x r y implies that y r x.). A relation that is reflexive, symmetric and transitive is an equivalence relation. in example 8.2.8 we proved that the relation given by (m, n) ∈ r ⇔ 3 ∣ (m − n) is an equivalence relation since we proved it is reflexive, symmetric, and transitive. A relation r is called reflexive on a set s if for all x ∈s, (x, x) ∈r. a relation r is called irreflexive on a set s if for all x ∈ s, (x , x ) ∉ r. a relation r is symmetric on a set s if for all x ∈ s and for all y ∈ s, if ( x , y ) ∈ r then ( y , x ) ∈ r. Reflexive: a relation is said to be reflexive, if (a, a) ∈ r, for every a ∈ a. symmetric: a relation is said to be symmetric, if (a, b) ∈ r, then (b, a) ∈ r. transitive: a relation is said to be transitive if (a, b) ∈ r and (b, c) ∈ r, then (a, c) ∈ r. in terms of equivalence relation notation, it is defined as follows: a binary. Worksheet 10: equivalence relations (1) for each of the following relation check whether it is reflexive symmetric or transitive: (1) e = { a,b ∈r 2 |a b = 350}. In particular, we define the reflexive, symmetric, and transitive properties. we will use directed graphs to identify the properties and look at how to prove whether a relation is reflexive, symmetric, and or transitive.

Reflexive Symmetric Transitive Equivalence Number Of Relations Aesl A relation r is called reflexive on a set s if for all x ∈s, (x, x) ∈r. a relation r is called irreflexive on a set s if for all x ∈ s, (x , x ) ∉ r. a relation r is symmetric on a set s if for all x ∈ s and for all y ∈ s, if ( x , y ) ∈ r then ( y , x ) ∈ r. Reflexive: a relation is said to be reflexive, if (a, a) ∈ r, for every a ∈ a. symmetric: a relation is said to be symmetric, if (a, b) ∈ r, then (b, a) ∈ r. transitive: a relation is said to be transitive if (a, b) ∈ r and (b, c) ∈ r, then (a, c) ∈ r. in terms of equivalence relation notation, it is defined as follows: a binary. Worksheet 10: equivalence relations (1) for each of the following relation check whether it is reflexive symmetric or transitive: (1) e = { a,b ∈r 2 |a b = 350}. In particular, we define the reflexive, symmetric, and transitive properties. we will use directed graphs to identify the properties and look at how to prove whether a relation is reflexive, symmetric, and or transitive.

Solved 2 ï Determine If The Following Relations R Are Chegg Worksheet 10: equivalence relations (1) for each of the following relation check whether it is reflexive symmetric or transitive: (1) e = { a,b ∈r 2 |a b = 350}. In particular, we define the reflexive, symmetric, and transitive properties. we will use directed graphs to identify the properties and look at how to prove whether a relation is reflexive, symmetric, and or transitive.

Relations Reflexive Symmetric Transitive Class 12 Mathematics
