Solved 1 Point The Following Series Are Geometric Series Chegg Arithmetic o geometric progression, an infinite series. finding the summation of such series. quick and shortest method to do that. no short tricks. full con. An arithmetic geometric progression (agp) is a progression in which each term can be represented as the product of the terms of an arithmetic progressions (ap) and a geometric progressions (gp).
Solved 1 ï Point ï The Following Series Are Geometric Series Chegg The nth term of an arithmetico–geometric sequence is the product of the n th term of an arithmetic sequence and the nth term of a geometric one. arithmetico–geometric sequences arise in various applications, such as the computation of expected values in probability theory. An arithmetico geometric series is the sum of consecutive terms in an arithmetico geometric sequence defined as: , where and are the th terms of arithmetic and geometric sequences, respectively. I was unable to find the formula for the sum of this series up to n terms. even this page only proves for a specific case of this series, as does my textbook. First suppose that sum of the series is s, then multiply it by common ratio of the g.p. and subtract. in this way, we shall get a g.p., whose sum can be easily obtained.
Solved 1 Point The Following Series Are Geometric Series Chegg I was unable to find the formula for the sum of this series up to n terms. even this page only proves for a specific case of this series, as does my textbook. First suppose that sum of the series is s, then multiply it by common ratio of the g.p. and subtract. in this way, we shall get a g.p., whose sum can be easily obtained. Given a particular term ai and the common difference d, find any other term, aj. given a1, d and some value x, determine which term in the sequence equals x. find the sum of the first n terms of the series. We have discussed the method to find the sum of n terms and the sum of infinite terms of any called arithmetic geometric series. we have also provided few solved examples based on this concept for more clarity. How to find the sum to infinity of a geometric series the sum to infinity of a geometric series is given by the formula s∞=a1 (1 r), where a1 is the first term in the series and r is found by dividing any term by the term immediately before it. We derive formulae for the partial and infinite sum of an arithmetico geometric sequence. we then apply the formula to an example, and conclude with an application to probability. more.
Solved The Following Series Are Geometric Series Or A Sum Of Chegg Given a particular term ai and the common difference d, find any other term, aj. given a1, d and some value x, determine which term in the sequence equals x. find the sum of the first n terms of the series. We have discussed the method to find the sum of n terms and the sum of infinite terms of any called arithmetic geometric series. we have also provided few solved examples based on this concept for more clarity. How to find the sum to infinity of a geometric series the sum to infinity of a geometric series is given by the formula s∞=a1 (1 r), where a1 is the first term in the series and r is found by dividing any term by the term immediately before it. We derive formulae for the partial and infinite sum of an arithmetico geometric sequence. we then apply the formula to an example, and conclude with an application to probability. more.
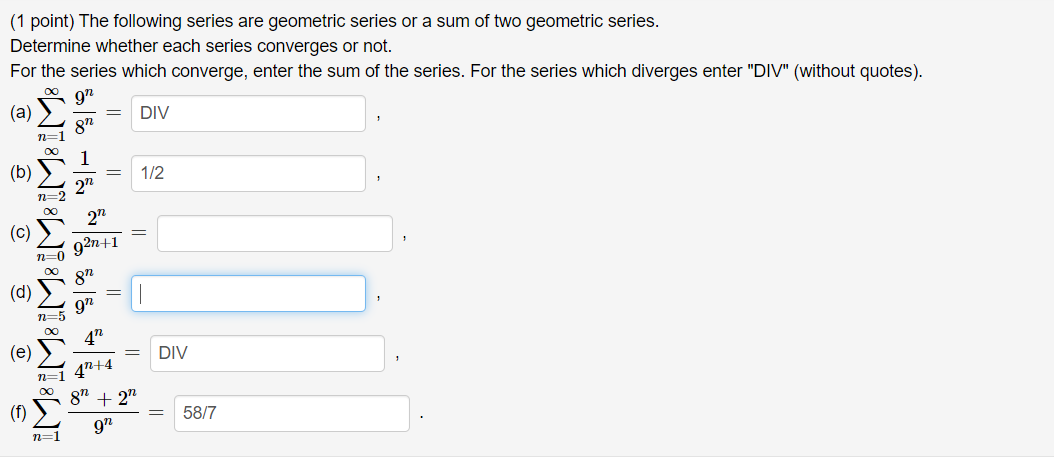
Solved The Following Series Are Geometric Series Or A Sum Of Chegg How to find the sum to infinity of a geometric series the sum to infinity of a geometric series is given by the formula s∞=a1 (1 r), where a1 is the first term in the series and r is found by dividing any term by the term immediately before it. We derive formulae for the partial and infinite sum of an arithmetico geometric sequence. we then apply the formula to an example, and conclude with an application to probability. more.
Solved The Following Series Are Geometric Series Or A Sum Of Chegg
Comments are closed.