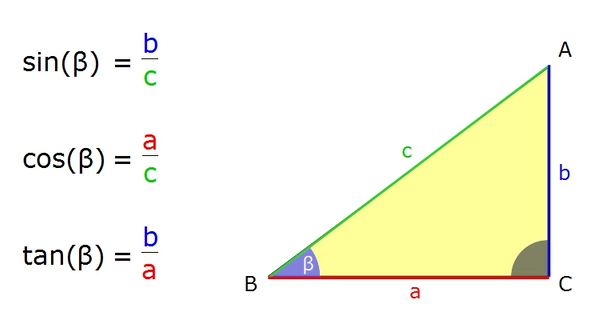
Sinus Kosinus Oder Tangens Anwenden Matheretter Voraussetzung ist, dass wir ein rechtwinkliges dreieck haben. nur dann können wir sinus, kosinus und tangens direkt anwenden. im folgenden die fälle, wann sinus, kosinus oder tangens anzuwenden sind: auch die winkel lassen sich bestimmen:. Wann genau muss ich sinus, kosinus und tangens anwenden? fehlende winkelgrößen mit sinus berechnen. gegeben sind 2 dreiecksseiten. in diesen mathe videos wird einfach erklärt, was sinus und kosinus sind und wie sie funktionieren. wir lernen, wie sie die berechnung von dreiecken vereinfachen.
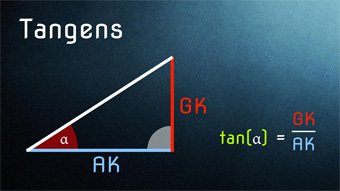
Sinus Kosinus Oder Tangens Anwenden Matheretter 5. tangens. 5.1 tangens einführung; 5.2 mögliche tangenswerte; 5.3 tangens als verhältnis von sinus kosinus; 5.4 tangens in den taschenrechner eingeben; 5.5 arkustangens: winkel aus tangenswert berechnen; 5.6 dreiecksseiten mit tangens bestimmen; 5.7 tangens am dreieck ablesen; 5.8 steigung einer linearen funktion mit tangens berechnen. Sinus kosinus oder tangens anwenden matheretter sinus, kosinus und tanges beschreiben die seitenverhältnisse in einem rechtwinkligen dreieck. hier kannst du lernen wie du winkel berechnest, sie sind die wichtigsten trigonometrischen funktionen. lerne die begriffe hypotenuse, gegenkathete und ankathete kennen!. Hat man nicht die gegenkathete, sondern die ankathete mit an bord, dann nutzt man den cosinus. ist die hypotenuse nicht weiters von belang, so bedient man sich des tangens. schau aber am besten einfach mal hier rein. Der tangens lässt sich über das verhältnis von gegenkathete zu ankathete ausdrücken, aber auch über ein verhältnis von sinus zu kosinus, wie wir im folgenden zeigen werden. schauen wir uns zuerst die definition von sinus an: \( \sin(β) = \frac{\text{gk}}{\text{hy}} \).
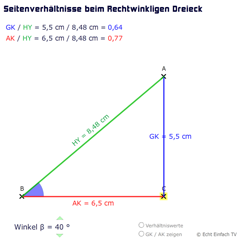
Lektion Tri04 Tangens Matheretter Hat man nicht die gegenkathete, sondern die ankathete mit an bord, dann nutzt man den cosinus. ist die hypotenuse nicht weiters von belang, so bedient man sich des tangens. schau aber am besten einfach mal hier rein. Der tangens lässt sich über das verhältnis von gegenkathete zu ankathete ausdrücken, aber auch über ein verhältnis von sinus zu kosinus, wie wir im folgenden zeigen werden. schauen wir uns zuerst die definition von sinus an: \( \sin(β) = \frac{\text{gk}}{\text{hy}} \). Die erste spalte steht für den sinus, die zweite für den kosinus, die dritte für den tangens und die vierte für den kotangens. beispiel: bei sinus steht g h also gegenkathete durch hypothenus. Du verwendest den sinus, wenn du den winkel und die länge der hypotenuse kennst und die länge der gegenüberliegenden seite berechnen möchtest. kosinus (cos): beschreibt das verhältnis der anliegenden seite zur hypotenuse. Der sinussatz im rechtwinkligen dreieck lautet ja: sin (alpha) = gegenkathete : hypotenuse. kosinus sinus tanges? das ist die aufgabe. die winkeln sind gegeben und die seitenlängen. nun muss ich tan sin oder cos anwenden. aber wie wende ich die an. zum beispiel muss ich jetztzu alpha eins anwenden. Du weißt doch sicherlich, dass der sinus die gegenkathete durch die hypotenuse und der kosinus die ankathete durch die hypotenuse ist. deine hypotenuse ist aber in dem fall b, weil der rechte winkel bei beta ist. und die gegenkathete des winkels alpha bzw. die ankathete des winkels beta ist eben a. =).
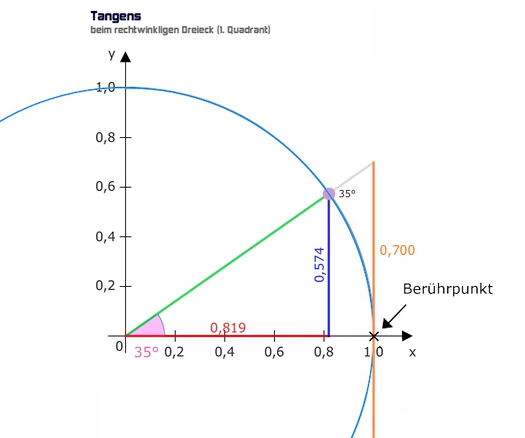
Tangens Wortherkunft Matheretter Die erste spalte steht für den sinus, die zweite für den kosinus, die dritte für den tangens und die vierte für den kotangens. beispiel: bei sinus steht g h also gegenkathete durch hypothenus. Du verwendest den sinus, wenn du den winkel und die länge der hypotenuse kennst und die länge der gegenüberliegenden seite berechnen möchtest. kosinus (cos): beschreibt das verhältnis der anliegenden seite zur hypotenuse. Der sinussatz im rechtwinkligen dreieck lautet ja: sin (alpha) = gegenkathete : hypotenuse. kosinus sinus tanges? das ist die aufgabe. die winkeln sind gegeben und die seitenlängen. nun muss ich tan sin oder cos anwenden. aber wie wende ich die an. zum beispiel muss ich jetztzu alpha eins anwenden. Du weißt doch sicherlich, dass der sinus die gegenkathete durch die hypotenuse und der kosinus die ankathete durch die hypotenuse ist. deine hypotenuse ist aber in dem fall b, weil der rechte winkel bei beta ist. und die gegenkathete des winkels alpha bzw. die ankathete des winkels beta ist eben a. =).
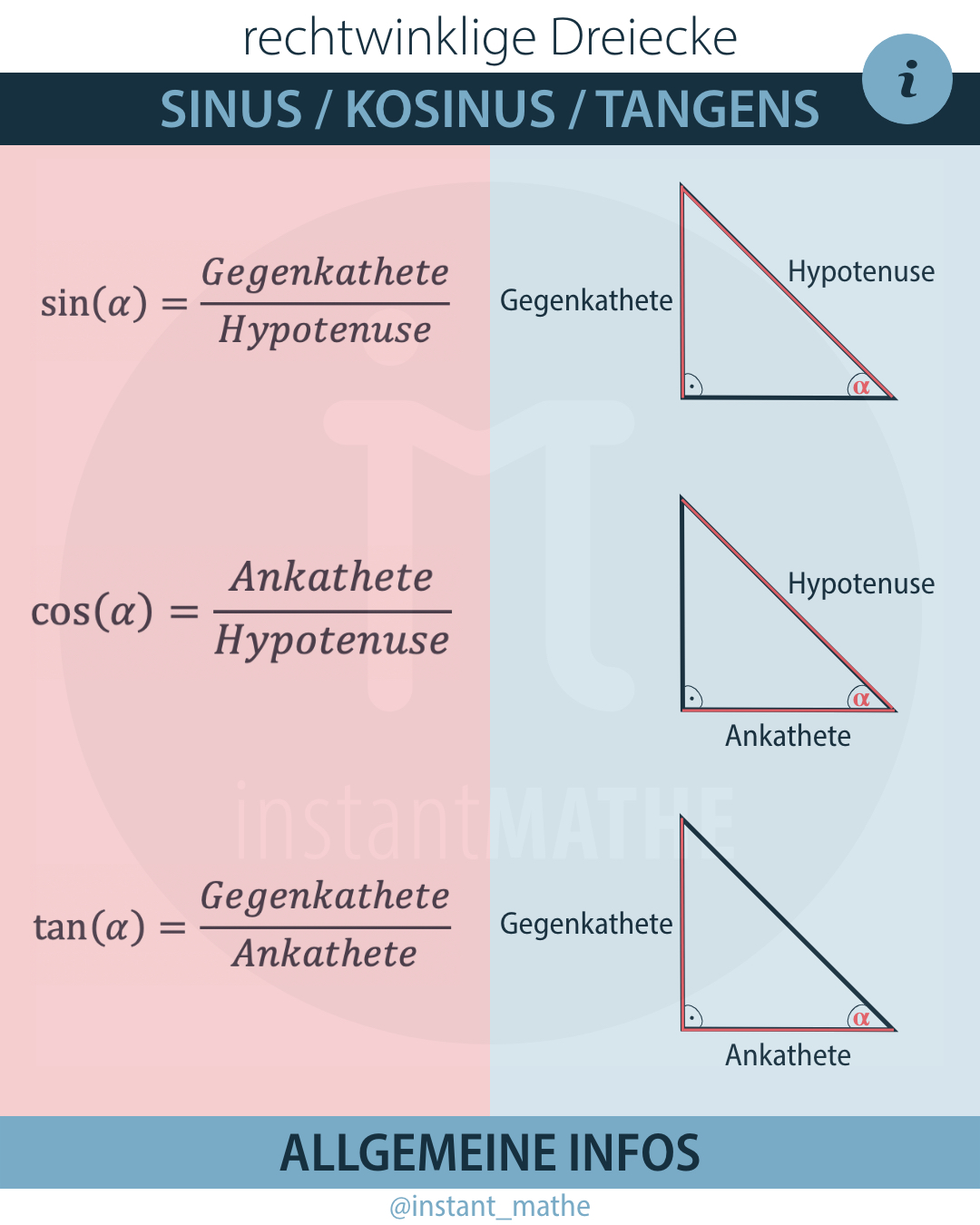
Trigonometrie Sinus Kosinus Tangens Online Berechnen Matheretter My Der sinussatz im rechtwinkligen dreieck lautet ja: sin (alpha) = gegenkathete : hypotenuse. kosinus sinus tanges? das ist die aufgabe. die winkeln sind gegeben und die seitenlängen. nun muss ich tan sin oder cos anwenden. aber wie wende ich die an. zum beispiel muss ich jetztzu alpha eins anwenden. Du weißt doch sicherlich, dass der sinus die gegenkathete durch die hypotenuse und der kosinus die ankathete durch die hypotenuse ist. deine hypotenuse ist aber in dem fall b, weil der rechte winkel bei beta ist. und die gegenkathete des winkels alpha bzw. die ankathete des winkels beta ist eben a. =).
Sinus Kosinus Oder Tangens Was Soll Man Anwenden Mathelounge
