
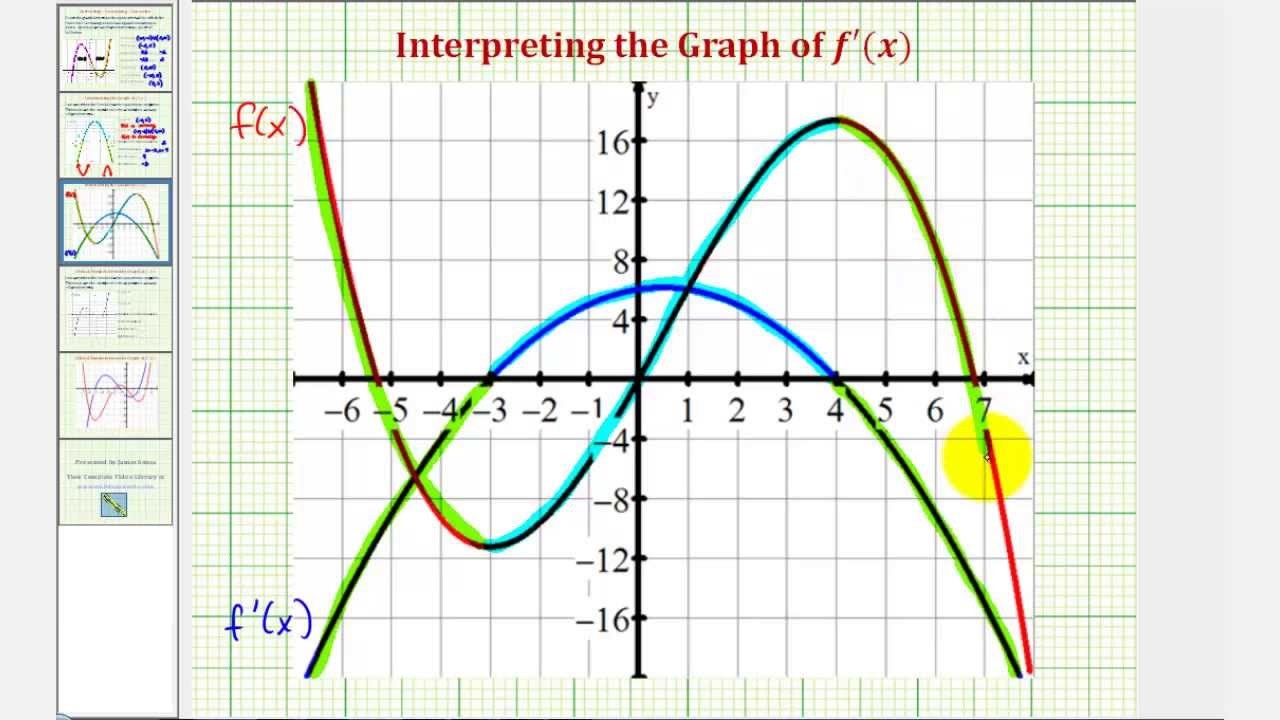
Sketching Derivatives From Parent Functions F F F Graphs F X This calculus video tutorial explains how to sketch the derivatives of the parent function using the graph f(x). this video contains plenty of examples and. Using the graph of f(x) = x3 — 6x2 ox, sketch the graph of f'(x) and f" (x) on the same axes. solution to sketch f'(x), begin by identifying the position of the local maximum and local minimum. through these points, draw vertical lines to separate the intervals where the slope of the tangent line is positive from.
Sketching Derivative Graphs At Paintingvalley Explore Collection 5.8 sketching graphs of functions and their derivatives: next lesson. packet. calc 5.8 packet.pdf: file size: 553 kb: file type: pdf: download file. want to save money on printing? support us and buy the calculus workbook with all the packets in one nice spiral bound book. solution manuals are also available. Real solution to f(x) = 0. call it r. could there be another root, s? if so, by rolle’s theorem, there would be a number c(between rand s) at which f0(c) = 0. to check, we compute the derivative of f(x) and see if it is ever equal to 0. we have f0(x) = 3x2 12x 15. to nd when f0(x) is 0, we solve the. Sketch the general shape of the graph of f(x) given the gradient function shcwn at right. i. determine the general ehape of the graph of ax) by raising the degree off'(x) by one. 2. locate the turning points, i.e. the x intercepts. (turning points occur when f'(x) = o.) 3. the magnitude and betwviour of the gradients. 4. sketch the general. Given a function f(x), there are several important features that we can determine from that expression before examining its derivatives. the domain of the function — take note of values where f does not exist. if the function is rational, look for where the denominator is zero.
Sketching Derivative Graphs At Paintingvalley Explore Collection Sketch the general shape of the graph of f(x) given the gradient function shcwn at right. i. determine the general ehape of the graph of ax) by raising the degree off'(x) by one. 2. locate the turning points, i.e. the x intercepts. (turning points occur when f'(x) = o.) 3. the magnitude and betwviour of the gradients. 4. sketch the general. Given a function f(x), there are several important features that we can determine from that expression before examining its derivatives. the domain of the function — take note of values where f does not exist. if the function is rational, look for where the denominator is zero. Learn how to identify where the derivative is 0, positive, and negative based on the graph of f (x) and create a sketch of the graph of the derivative, f’ (x). i will take you. The transition from f(x) to f'(x) and subsequently to f''(x) focuses on understanding slopes and their interpretations in graphical forms. recognizing how to sketch the derivatives through analyzing slopes, critical points, and concavity plays a pivotal role in understanding the function's behavior. In figure \(4.3\) we show the functions \(y(t)\) (top row), their first derivatives \(y^{\prime}(t)\) (middle row), and the second derivatives \(y^{\prime \prime}(t)\) (bottom row). in each case, we determined the slopes of tangent lines as a first step. 📉 the graph of f'(x) can be determined by analyzing the increasing and decreasing nature of f(x), as the slope of f(x) becomes the y values of f'(x). 🔄 the second derivative, f''(x), can be found by differentiating f'(x), and it provides information about the concavity of the function.
