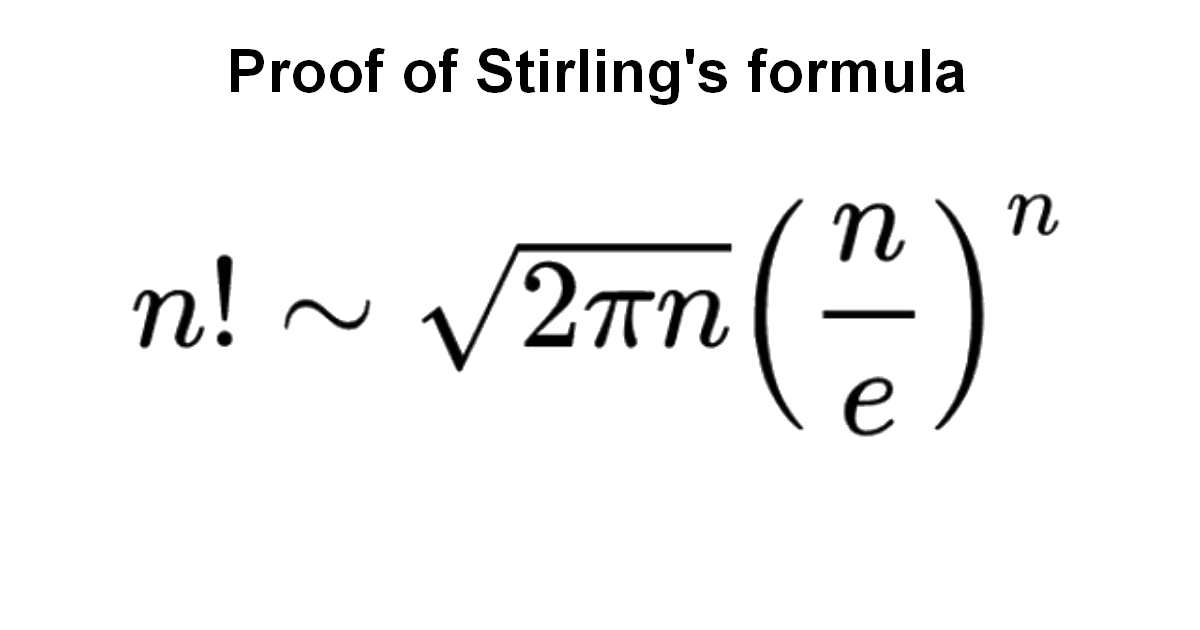
Solution Proof Stirling Formula Art Of Mathematics Stirling’s approximation is an important approximation for factorials. it is leading to accurate results even for small values of \ (n\). it is named after james stirling, though it was first stated by abraham de moivre. first, we know that \ (n!=1\cdot2\cdot\cdot\cdot n\). Proof stirling's formula get the solution related topics: solved problems how far apart are the poles ? solution why 0.9999999 =1 solution find the.

Solution Proof Stirling Formula Art Of Mathematics The factorial function can be approximated by the formula: $n! \sim \sqrt {2 \pi n} \paren {\dfrac n e}^n$ where $\sim$ denotes asymptotically equal. refinement. a refinement of stirling's formula is: $n! = \sqrt {2 \pi n} \paren {\dfrac n e}^n \paren {1 \dfrac 1 {12 n} \map \oo {\dfrac 1 {n^2} } }$ proof 1. Stirling’s formula provides an approximation to n! which is relatively easy to compute and is sufficient for most purposes. using it, one can evaluate log n! to better and better accuracy as n becomes large, provided that one can evaluate log n as accurately as needed. then to compute b(k,n,p) := n k. Here are a couple of "proofs" of stirling's formula. they are quite elegant (in my opinion), but not rigorous. on could write down a real proof from these, but as they rely on some hidden machinery, the result would be quite heavy. 1) a probabilistic non proof. we start from the expression $e^{ n} n^n n!$, of which we want to find an equivalent. We present a short proof of stirling’s formula that uses only a basic knowledge of calculus. 1. introduction. numerous proofs [1, 2, 3, 6, 7, 8] of stirling’s formula of varying levels of sophistication have appeared in the literature.

Solution Proof Stirling Formula Art Of Mathematics Here are a couple of "proofs" of stirling's formula. they are quite elegant (in my opinion), but not rigorous. on could write down a real proof from these, but as they rely on some hidden machinery, the result would be quite heavy. 1) a probabilistic non proof. we start from the expression $e^{ n} n^n n!$, of which we want to find an equivalent. We present a short proof of stirling’s formula that uses only a basic knowledge of calculus. 1. introduction. numerous proofs [1, 2, 3, 6, 7, 8] of stirling’s formula of varying levels of sophistication have appeared in the literature. In upper limit on the central binomial coefficient, noam elkies and david speyer have given a nice proof that the central binomial coefficient . this can be used to derive stirling's formula an = n!en nn√n ∼ √2π by showing that an is decreasing, hence convergent to some positive real number c, and computing c via c = lim n → ∞ a2n a2n = √2π. What form of stirling do you need? n.s. gives the simplest above, and you can get even better without sacrificing a ton of simplicity for example, if you drop the condition of needing to know the multiplicative constant (2π−−√ 2 π) a proof is a lot easier. why is 2π−−√ 2 π usually included if one can just use the version n.s. showed?. Theorem: if a function f(x) satisfies the following three conditions then it is identical to the gamma function. proof: suppose f(x) satisfies the three properties. then since f(1)=1 and f(x 1)=xf(x), for integer n≥2, f(x n)=(x n 1)(x n 2) (x 1)xf(x) f(n) = (n 1)! proof: suppose f(x) satisfies the three properties. I need to gain understanding of a proof of stirling's formula. i have read through tim gowers' and terence tao's but i'm struggling to follow them. how rigorous is this proof, if at all?.

Solution Proof Stirling Formula Art Of Mathematics In upper limit on the central binomial coefficient, noam elkies and david speyer have given a nice proof that the central binomial coefficient . this can be used to derive stirling's formula an = n!en nn√n ∼ √2π by showing that an is decreasing, hence convergent to some positive real number c, and computing c via c = lim n → ∞ a2n a2n = √2π. What form of stirling do you need? n.s. gives the simplest above, and you can get even better without sacrificing a ton of simplicity for example, if you drop the condition of needing to know the multiplicative constant (2π−−√ 2 π) a proof is a lot easier. why is 2π−−√ 2 π usually included if one can just use the version n.s. showed?. Theorem: if a function f(x) satisfies the following three conditions then it is identical to the gamma function. proof: suppose f(x) satisfies the three properties. then since f(1)=1 and f(x 1)=xf(x), for integer n≥2, f(x n)=(x n 1)(x n 2) (x 1)xf(x) f(n) = (n 1)! proof: suppose f(x) satisfies the three properties. I need to gain understanding of a proof of stirling's formula. i have read through tim gowers' and terence tao's but i'm struggling to follow them. how rigorous is this proof, if at all?.
