
The Sum And The Product Of Roots Of Quadratic Equations Pdf Finding the sum and product of the roots of a cubic equations: an equation in which at least one term is raised to the power of 3 but no term is raised to any higher power is called a cubic equation. the general form of a cubic equation is ax 3 bx 2 cx d = 0 where a, b, c and d are constants and a ≠ 0. Chapter 1 theory of equations 4 1.2 the roots of a quadratic equation given a quadratic function y= ax2 bx c. if we set y= 0, we obtain ax2 bx c= 0, which is a quadratic equation. the solutions (roots) of it can be found readily from equation (1.1). a x b 2a 2 = 4a ( = b2 4ac) x b 2a = r 4a2 x = b 2a p 2a x = b p 2a properties of the roots.

Sum And Product Of Quadratic Equation Roots With Examples Quadratic equation: sum and product of roots: the solutions or the roots of the above quadratic equation can be given by quadratic formula as : and is denoted by d or Δ. the relationship is given as: sum of roots. the product of roots is given by ratio of the constant term and the coefficient of. let us try to prove this graphically. Given a cubic or quartic equation, we will explain how to solve it with pure thought. this should convince you that you could write down the solution in radicals if you wanted to. to start, we explain how one might solve the cubic equation. suppose we start with an equation of the form. x3 x2 x . Sum of the roots = −b a = b; product of the roots = c a = c; which gives us this result. x 2 − (sum of the roots)x (product of the roots) = 0. the sum of the roots is 10, and product of the roots is 23, so we get: x 2 − 10x 23 = 0. and here is its plot: (question: what happens if we choose a=−1?). Free lesson on sums and products of roots (quadratic, cubic and quartic), taken from the polynomials topic of our ontario canada (11 12) grade 12 textbook. learn with worked examples, get interactive applets, and watch instructional videos.
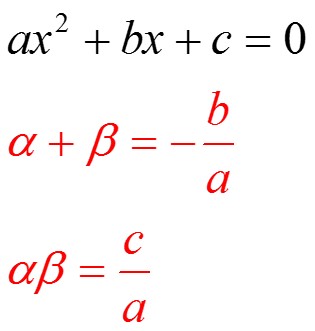
Sum And Product Of Roots Of A Quadratic Equation Mathexams Sum of the roots = −b a = b; product of the roots = c a = c; which gives us this result. x 2 − (sum of the roots)x (product of the roots) = 0. the sum of the roots is 10, and product of the roots is 23, so we get: x 2 − 10x 23 = 0. and here is its plot: (question: what happens if we choose a=−1?). Free lesson on sums and products of roots (quadratic, cubic and quartic), taken from the polynomials topic of our ontario canada (11 12) grade 12 textbook. learn with worked examples, get interactive applets, and watch instructional videos. Find the sum and product of roots of a given quadratic equation without solving it. roots satisfy a given relation (e.g., the relation \ [2 (\alpha) 5 (\beta) = 7, where (\alpha) and (\beta)\] are the roots of the given equation. both sum and product of roots are equal to a given number. (i) the document contains solutions to exercises involving finding cube roots, sums and products of roots of quadratic equations, and determining values of parameters for which certain relationships between roots are satisfied. So we can apply the quadratic formula immediately. here a = 1 ,'b = 4, c = 1, substituting these values in the quadratic formula, we get the two roots of the equation to be. x = 4 4 1) (1 4 fi a 2 = 2 fi and 2(1) thus, the solutions are 2 6 and 2 fi , in = = = = , and \. Given a quadratic equation, we can evaluate the sum and product of its roots using these expressions. here are two examples (we will use \(\alpha \) and \(\beta \) to denote the two roots):.

Sum And Product Of Roots Of Quadratic Equation 3 By Mathamaniacs Find the sum and product of roots of a given quadratic equation without solving it. roots satisfy a given relation (e.g., the relation \ [2 (\alpha) 5 (\beta) = 7, where (\alpha) and (\beta)\] are the roots of the given equation. both sum and product of roots are equal to a given number. (i) the document contains solutions to exercises involving finding cube roots, sums and products of roots of quadratic equations, and determining values of parameters for which certain relationships between roots are satisfied. So we can apply the quadratic formula immediately. here a = 1 ,'b = 4, c = 1, substituting these values in the quadratic formula, we get the two roots of the equation to be. x = 4 4 1) (1 4 fi a 2 = 2 fi and 2(1) thus, the solutions are 2 6 and 2 fi , in = = = = , and \. Given a quadratic equation, we can evaluate the sum and product of its roots using these expressions. here are two examples (we will use \(\alpha \) and \(\beta \) to denote the two roots):.

Solution Theory Of Quadratic Equation Cubic Roots Sum And Product Of So we can apply the quadratic formula immediately. here a = 1 ,'b = 4, c = 1, substituting these values in the quadratic formula, we get the two roots of the equation to be. x = 4 4 1) (1 4 fi a 2 = 2 fi and 2(1) thus, the solutions are 2 6 and 2 fi , in = = = = , and \. Given a quadratic equation, we can evaluate the sum and product of its roots using these expressions. here are two examples (we will use \(\alpha \) and \(\beta \) to denote the two roots):.
