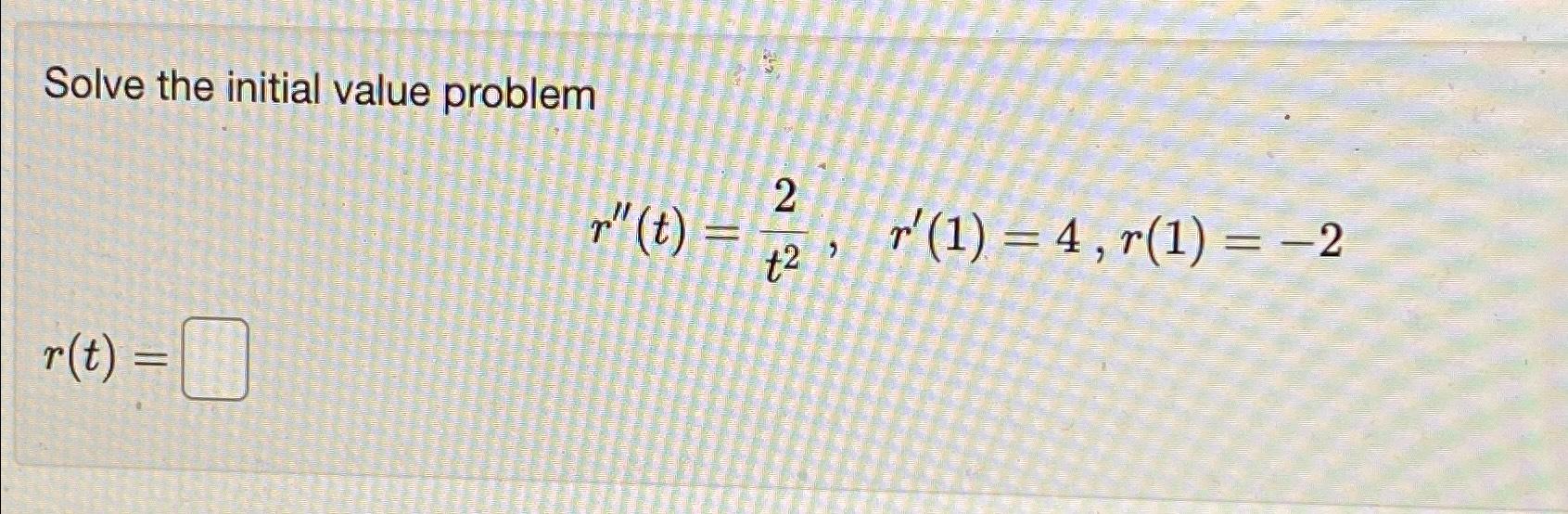
Solved Solve The Initial Value Chegg Chapter 4.8 antiderivatives ex107 109數學系卡安很閒 所以決定拯救沒辦法用quizlet和chegg的莘莘學子support me : ko fi aliceryugusolve the initial value problems in. Finding integrals: to solve the problem, we integrated 2 t 3 to get the first derivative d r d t, and then integrated that result to find r (t). each step involved calculating the integral of a part of the equation.
Solved Initial Value Problems Solve The Initial Value Chegg There are 2 steps to solve this one. to solve the initial value problem for the given second order differential equation d 2 r d t 2 = 2 t 3 with initial co not the question you’re looking for? post any question and get expert help quickly. This page titled 8.3e: solution of initial value problems (exercises) is shared under a cc by nc sa 3.0 license and was authored, remixed, and or curated by william f. trench. Goals the goal of this section is to use laplace transform to solve initial value problems, second order linear equations (as in §3.1, 3.3, 3.4, 3.5, 3.6). this way, the methods may become more algebraic. two theorem that follows would be instrumental for this method. A differential equation together with one or more initial values is called an initial value problem. the general rule is that the number of initial values needed for an initial value problem is equal to the order of the differential equation.
Solved Solve The Initial Value Problem Dr D R 2 Dt2 3 5 Chegg Goals the goal of this section is to use laplace transform to solve initial value problems, second order linear equations (as in §3.1, 3.3, 3.4, 3.5, 3.6). this way, the methods may become more algebraic. two theorem that follows would be instrumental for this method. A differential equation together with one or more initial values is called an initial value problem. the general rule is that the number of initial values needed for an initial value problem is equal to the order of the differential equation. The initial value problems in examples 1, 2, and 3 each had a unique solution; values for the arbitrary constants in the general solution were uniquely determined. Having explored the laplace transform, its inverse, and its properties, we are now equipped to solve initial value problems (ivp) for linear differential equations. This section applies the laplace transform to solve initial value problems for constant coefficient second order differential equations on (0,∞). An initial value problem (ivp) involves solving a differential equation where the solution must satisfy specific conditions at a given point. this helps identify a unique solution from a family of possible solutions.
Comments are closed.