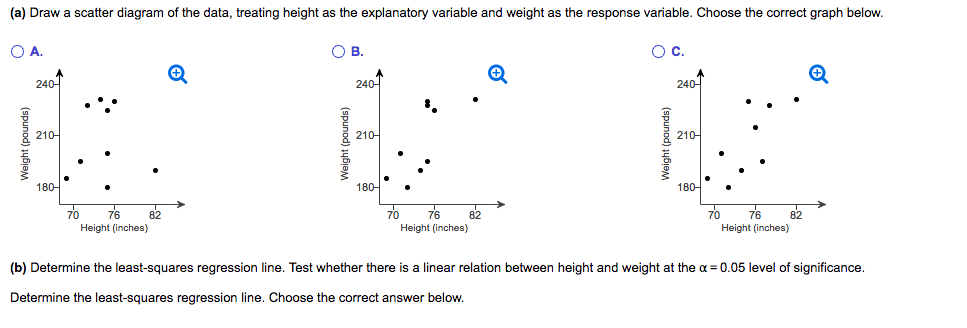
Solved 06 Question 5 Points Player 1 And Player 2 Are Chegg

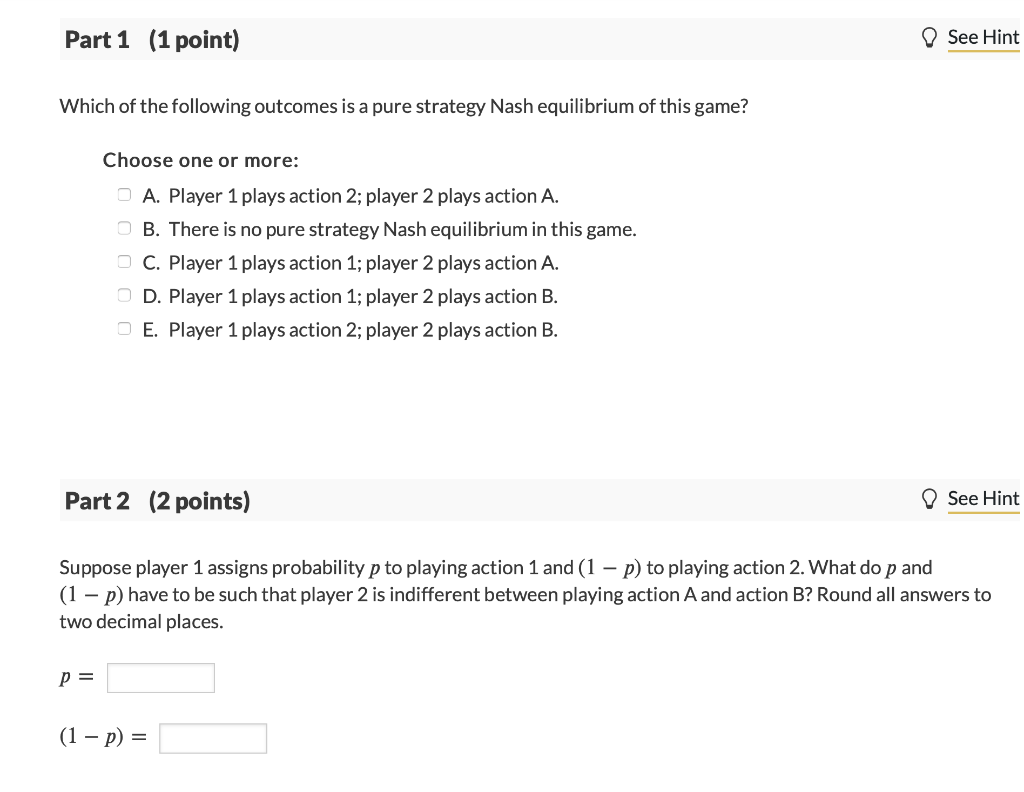
Solved Player Player 1 Player 2 Player 3 Player 4 Player 5 Chegg Question: 06 question (5 points) player 1 and player 2 are playing a simultaneous move one shot game, where player 1 can perform action 1 or action 2 and player 2 can perform action a or action b. The actions and payos of the game are given by left right up 0, 4 1, 1 down 1, 2 t, 4 where the row player is player 1. we will use the following notation: σ1 (t) is the probability that player 1 plays up if she is of type t; σ2 is the probability that player 2 plays left.

Solved 06 Question 5 Points Player 1 And Player 2 Are Chegg Player 1 and player 2 are playing a game in which player 1 has the first move at a in the decision tree shown below. once player 1 has chosen either up or down, player 2, who can see what player 1 has chosen, must choose up or down at b or c. Consider a game in which, simultaneously, player 1 selects any real number x and player 2 selects any real number y. the payoffs are given by: u1 (x,y) = 2x x^2 2xy and u2 (x,y) = 10y 2xy y^2. Player 1 and player 2, henceforth called p 1, and p 2 respectively are in competion with each other. the winner of the competion is the player who wins the most number of games (not the player with the cloestest ratio of wins:loses being 1:1). Consider an integer game between two players: marilyn and noah. each of the player is required to announce a positive integer. in other words, a player can announce 1, 2, 3, 4, 5 , but cannot announce "infinity". two players announce their integers simultaneously.

Solved 06 Question 5 Points Player 1 And Player 2 Are Chegg Player 1 and player 2, henceforth called p 1, and p 2 respectively are in competion with each other. the winner of the competion is the player who wins the most number of games (not the player with the cloestest ratio of wins:loses being 1:1). Consider an integer game between two players: marilyn and noah. each of the player is required to announce a positive integer. in other words, a player can announce 1, 2, 3, 4, 5 , but cannot announce "infinity". two players announce their integers simultaneously. Finally, if player 1 chooses south and player 2 chooses east, then player 1 receives a payoff of 1, and player 2 receives a payoff of 16. use this information to answer the questions below. Explanation: if player 2 selects strategy t1, then for s1 strategy selected by an opponent, he is having payoffs 10 which is optimal. however, if the opponent selects s2, then player 2 will get a payoff of 0 which is not an optimal option. hence, t1 is not the dominant strategy for player 2. In this game, called matching pennies, player 1 wins if both players play the same side of a penny, and player 2 wins if the players play opposite sides of a penny. If we see group 2, there was only one match between player 20 and 50 and they both scored 5 points each. when there is a tie like this, the winner is with lowes player id.

Solved 06 Question 5 Points Player 1 And Player 2 Are Chegg Finally, if player 1 chooses south and player 2 chooses east, then player 1 receives a payoff of 1, and player 2 receives a payoff of 16. use this information to answer the questions below. Explanation: if player 2 selects strategy t1, then for s1 strategy selected by an opponent, he is having payoffs 10 which is optimal. however, if the opponent selects s2, then player 2 will get a payoff of 0 which is not an optimal option. hence, t1 is not the dominant strategy for player 2. In this game, called matching pennies, player 1 wins if both players play the same side of a penny, and player 2 wins if the players play opposite sides of a penny. If we see group 2, there was only one match between player 20 and 50 and they both scored 5 points each. when there is a tie like this, the winner is with lowes player id.