
Solved Let B 1 2 3 4 5 And Chegg Let a = {1, 2, 3, 4, 5} and b = {1, 2, 3, 4, 5}. consider the following relations: which of the following are one to one from a to b ? which of the following are onto from a to b ?. Given, a = {1, 2}, b = {2, 3, 4} and c = {4, 5} (i) b ∩ c = {2, 3, 4} ∩ {4, 5} = {4} ∴ a × (b ∩ c) = {1, 2} × {4} = { (1, 4), (2, 4)} (ii) b ∪ c = {2, 3, 4} ∪ {4, 5} = {2, 3, 4, 5} ∴ a × (b ∪ c) = {1, 2} × {2, 3, 4, 5} = { (1, 2), (1, 3) (1, 4), (1, 5), (2, 2), (2, 3), (2, 4), (2, 5)} let a = (1, 2}, b = {2, 3, 4}, c = {4, 5}.

Solved 3 Let A 1 2 3 4 5 6 And 1 2 3 4 5 6 P1 Chegg ∴ the total number of possible relations = 2 × 2 × 2 × 2 × 2 = 2 5. but since, every element of the range must be related to at least one element of the domain, we need to subtract the cases where all elements of a are linked to either {a} only or {b} only, which is 1 for each case. Solve an equation, inequality or a system. what can quickmath do? quickmath will automatically answer the most common problems in algebra, equations and calculus faced by high school and college students. the algebra section allows you to expand, factor or simplify virtually any expression you choose. Free math problem solver answers your algebra homework questions with step by step explanations. Let a= 1,2,3,4,5 and b= 0,3,6 find a) a∪ b. b) a∩ b. c) a b. d) b a. 14. find the sets a and bifa b= 1,5,7,8 ,b a= 2,10 and a∩ b= 3,6,9 . 15. prove the second de morgan law in table 1 by showing that if a and b are sets, then overline a∪ b=overline a∩ overline b a) by showing each side is a subset of the other side. to solve the.
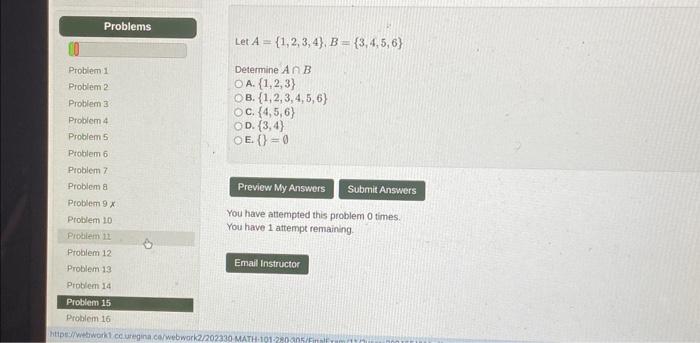
Solved Let A 1 2 3 4 B 3 4 5 6 Determine Aв B A 1 2 3 Chegg Free math problem solver answers your algebra homework questions with step by step explanations. Let a= 1,2,3,4,5 and b= 0,3,6 find a) a∪ b. b) a∩ b. c) a b. d) b a. 14. find the sets a and bifa b= 1,5,7,8 ,b a= 2,10 and a∩ b= 3,6,9 . 15. prove the second de morgan law in table 1 by showing that if a and b are sets, then overline a∪ b=overline a∩ overline b a) by showing each side is a subset of the other side. to solve the. Let a = {1, 2, 3, 4, 5} and b = {1, 2, 3, 4, 5, 6}. then the number of functions f : a → b satisfying f (1) f (2) = f (4) – 1 is equal to. Example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. find a × (b ∩ c) b ∩ c = {3, 4} ∩ {"4, 5, 6" } = {"4" } a × (b ∩ c) = {"1, 2, 3" } × {"4" } = {"(1, 4), (2, 4), (3, 4)" } ∩ intersection : common between two sets example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. To find the intersection of two sets, we look for elements that are present in both sets. the intersection of sets, denoted as a ∩ b, consists of all elements that belong to both set a and set b. given sets: a = {1, 2, 3, 4, 5} b = {2, 4} step by step process to find a ∩ b: list the elements of set a: 1 ; 2 ; 3 ; 4 ; 5; list the elements of. A = {1, 2, 3, 5} and b = {4, 6, 9}. define a relation r from a to b by r = {(x, y): the difference between x and y is odd; x ∈ a, y ∈ b}. write r in roster form. let a = {1, 2, 3, 4, 6}. let r be the relation on a defined by {(a, b): a, b ∈ a, b is exactly divisible by a}. write r in roster form; find the domain of r; find the range of r.
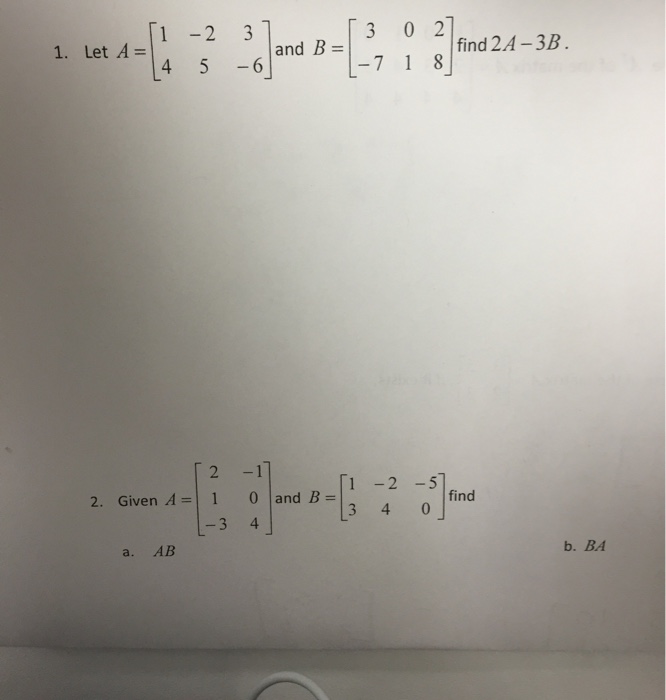
Solved Let A 1 4 2 5 3 6 And B 3 7 0 1 2 8 Find Chegg Let a = {1, 2, 3, 4, 5} and b = {1, 2, 3, 4, 5, 6}. then the number of functions f : a → b satisfying f (1) f (2) = f (4) – 1 is equal to. Example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. find a × (b ∩ c) b ∩ c = {3, 4} ∩ {"4, 5, 6" } = {"4" } a × (b ∩ c) = {"1, 2, 3" } × {"4" } = {"(1, 4), (2, 4), (3, 4)" } ∩ intersection : common between two sets example 3 let a = {1, 2, 3}, b = {3, 4} and c = {4, 5, 6}. To find the intersection of two sets, we look for elements that are present in both sets. the intersection of sets, denoted as a ∩ b, consists of all elements that belong to both set a and set b. given sets: a = {1, 2, 3, 4, 5} b = {2, 4} step by step process to find a ∩ b: list the elements of set a: 1 ; 2 ; 3 ; 4 ; 5; list the elements of. A = {1, 2, 3, 5} and b = {4, 6, 9}. define a relation r from a to b by r = {(x, y): the difference between x and y is odd; x ∈ a, y ∈ b}. write r in roster form. let a = {1, 2, 3, 4, 6}. let r be the relation on a defined by {(a, b): a, b ∈ a, b is exactly divisible by a}. write r in roster form; find the domain of r; find the range of r.
