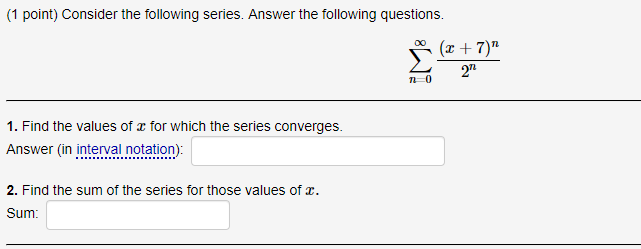
Solved 1 Point Consider The Following Series Answer The Chegg For each of the following series, determine whether the series converges or diverges. you must state any test you are using and clearly justify any conditions and validate your conclusions. a a) does this series converge? is the convergence conditional or absolute? ( 1)" vn 1 2. nat c) does the series converge? n=1 00 d) does this series. Math 115 exam #1 practice problems for each of the following, say whether it converges or diverges and explain why. 1. p ∞ n=1 n3 5 3 answer: notice that n3 n5 3 < n3 n5 = 1 n2 for all n. therefore, since p 1 n2 converges (it’s a p series with p = 2 > 1), the series p n3 n5 3 also converges by the comparison test. 2. p ∞ n=1 3n 4n 4.
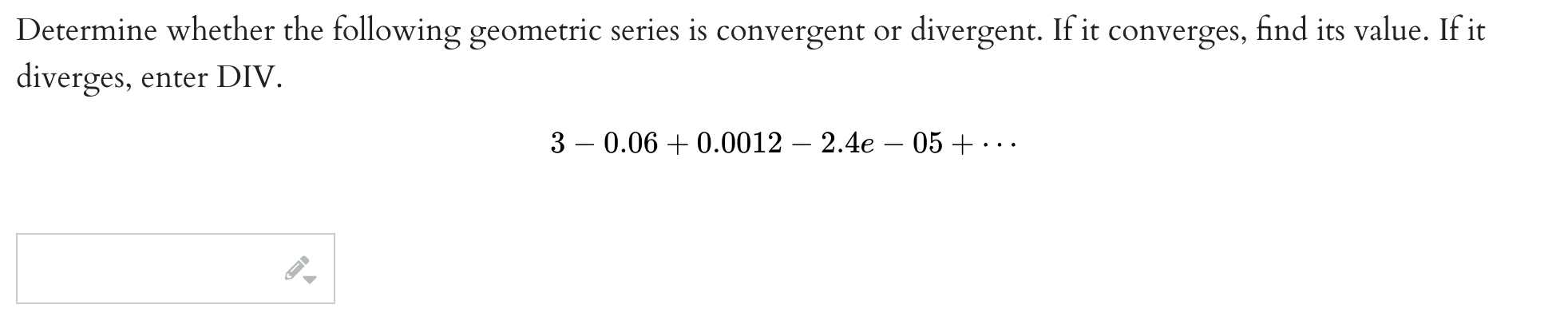
Solved Consider The Following Series Answer The Following Chegg With the q&a solutions search engine, you can copy and paste a chegg, course hero or homework question, and get an instant answer. start now by copy and pasting the entire homework question into the ‘type your message’ box, below: hello. what is your homework question?. Test each of the following series for convergence by either the comparison test or the limit comparison test. if at least one test can be applied to the series, enter conv if the series converges or div if it diverges. if neither test can be applied to the series, enter na. For each of the following, determine whether the series is convergent or divergent. if it is convergent, find its sum. a) ∑ n = 1 ∞ 4 n − 1 ( − 3 ) n − 1 answer: (i) the series converges diverges (circle one) (ii) sum (if exists) = b) ∑ n = 1 ∞ 3 n 6 ⋅ 2 2 n − 2 answer: (i) the series converges diverges (circle one) (ii) sum. 1 p n 4 first, we show the absolute series is divergent. note that x1 n=1 1 p n 4 ˇ x1 n=1 1 p n which is a divergent p series with p= 1 2 <1. next, check: lim n!1 1 p n 4 1 p n = lim n!1 p n 4 = lim n!1 1 1 4 p n = 1 which is nite and non zero. therefore, these two series share the same behavior. since x1 n=1 1 p n is the divergent p.

Solved Consider The Following Series Answer The Following Chegg For each of the following, determine whether the series is convergent or divergent. if it is convergent, find its sum. a) ∑ n = 1 ∞ 4 n − 1 ( − 3 ) n − 1 answer: (i) the series converges diverges (circle one) (ii) sum (if exists) = b) ∑ n = 1 ∞ 3 n 6 ⋅ 2 2 n − 2 answer: (i) the series converges diverges (circle one) (ii) sum. 1 p n 4 first, we show the absolute series is divergent. note that x1 n=1 1 p n 4 ˇ x1 n=1 1 p n which is a divergent p series with p= 1 2 <1. next, check: lim n!1 1 p n 4 1 p n = lim n!1 p n 4 = lim n!1 1 1 4 p n = 1 which is nite and non zero. therefore, these two series share the same behavior. since x1 n=1 1 p n is the divergent p. L2. (a) state, with justification, whether each of the following series converges or diverges. (i) \sum (n=1)^(\infty ) (n) (3n 1) (ii) [6 marks] (b) calculate all fourth roots of . 1 i. in c , eqpessing your answers in polar form. [ 6 marks] (c) use the cauchy riemman equations to determine where the complex function solved on time. For each of the following power series, find the interval of convergence and the radius of convergence: notice that an 1 = (−1)n 1(n 1)2xn 1. then lim n→∞. 1)2|x|n 1 = lim n2|x|n n→∞ |x| 2n 2 2 = |x| lim = n→∞ 2n |x| lim = |x|, so this series converges absolutely for n→∞ 2 −1 < x < 1. (−1)nn2 which diverges by the nth term test. 1. [4 points] suppose that the power series x∞ n=0 c n(x− 3)n converges at x = 6 and diverges at x= −2. what can you say about the behavior of the power series at the following values of x? for each part, circle the correct answer. ambiguous responses will be marked incorrect. a. [1 point] at x= −3, the power series converges. For each of the following series, choose the first listed reason why the series diverges. a. ∑ n = 1 ∞ 2 4 2 n b. ∑ n = 1 ∞ 1 − n 1 c. ∑ n = 1 ∞ n 2 − 1 n d. ∑ n = 1 ∞ n! n n 1. the series diverges by the divergence test. 2. the series is a divergent geometric series. 3. the series is a divergent p series. 4.
