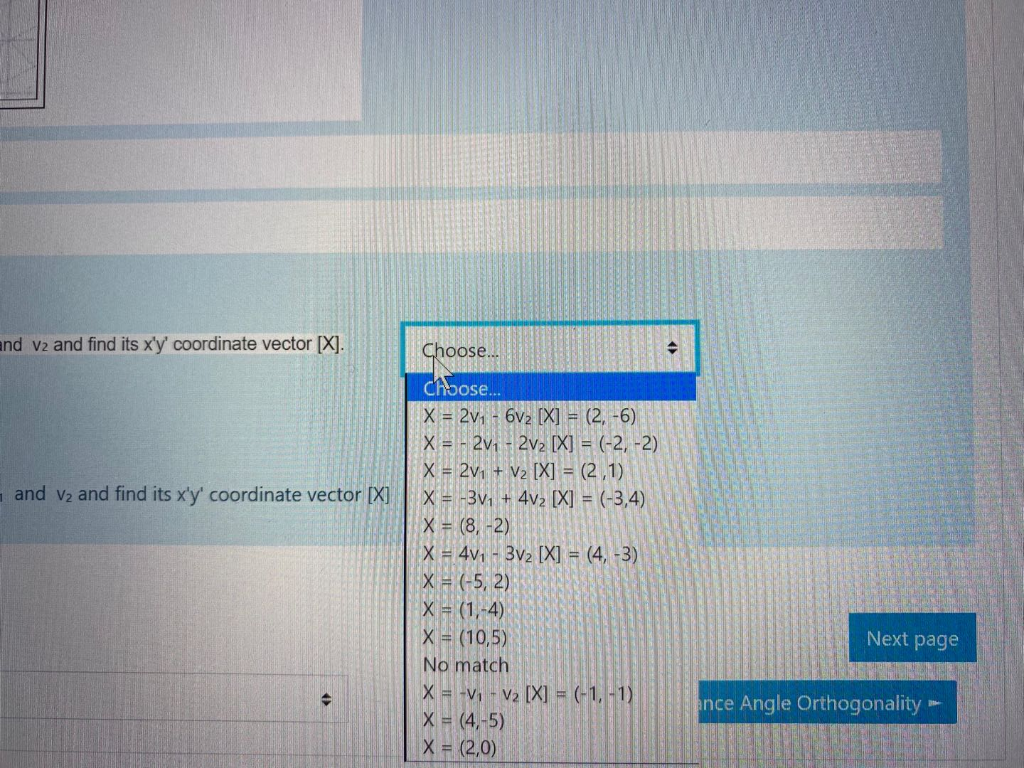
Solved 1 Given The Basis B V1 V2 Of R2 With Associated Chegg Question: 1 given the basis b = v1 = ,v2 of r2 with associated x'y' coordinate system shown in the figure below. in the following questions [x] is [x]g = [x]x'y', the coordinate vector of x relative to the basis b, which also is the x'y' coordinate vector of x. find a matching answer from the given choices for each of the following. Let b= {v1,v2} be a basis of r2 where v1= (1,1) and v2= (−1,0). (a) find a vector w∈r2 (relative to the standard basis) such that [w]b= (4,7). (b) find the b coordinates [u]b of the vector u= (−2,5) where u is given relative to the standard basis.

Solved Given The Basis B V1 1 1 V2 21 Of R2 With Chegg The first thing you did is put each new basis vector in b′ = {v1,v2,v3} b ′ = {v 1, v 2, v 3} in terms of your original basis b = {u1,u2,u3} b = {u 1, u 2, u 3}. The given set {v1,v2} is a basis for r2. how to determine if set is a basis of vector space? assume that for some n, v is a subspace of rn. a collection of vectors from v, b = {v1, v2, vr}, is said to be a basis for v, if b spans v and is linearly independent. the collection cannot serve as a basis for v if either of these conditions is not met. Question: given the basis b= {v1= [−1−1],v2= [−21]} of r2 with associated x′y′ coordinate system shown in the figure below. in the following questions [x] is [x]b= [x]x′y′, the coordinate vector of x relative to the basis b, which also is the x′y′ coordinate vector of x. find a matching answer from the given choices for. Video answer: we need to change the basis from the standard basis to the basis b dash to find the matrix a dash for t. the b dash will be marked as b1, b2, and b3 with the help of the columns of a dash.
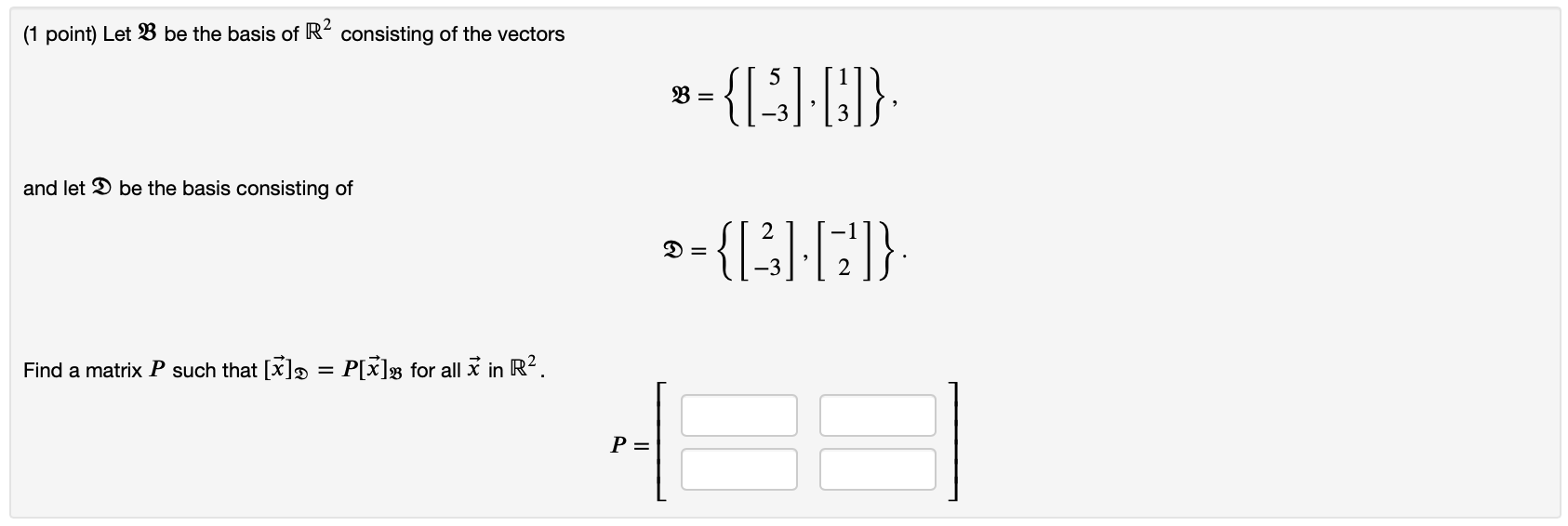
Solved 1 Point Let B Be The Basis Of R2 Consisting Of The Chegg Question: given the basis b= {v1= [−1−1],v2= [−21]} of r2 with associated x′y′ coordinate system shown in the figure below. in the following questions [x] is [x]b= [x]x′y′, the coordinate vector of x relative to the basis b, which also is the x′y′ coordinate vector of x. find a matching answer from the given choices for. Video answer: we need to change the basis from the standard basis to the basis b dash to find the matrix a dash for t. the b dash will be marked as b1, b2, and b3 with the help of the columns of a dash. Let v1 = (1, 4, 5), v2 = (2, 3, 1), and v3 = ( 4, 1, 7) (write as column vectors). why does b = {v1, v2, v3} form a basis for ℝ^3? we need to show that b is a linearly independent set of. Let the basis b = {v1,v2} be a basis of r2, where v1 =[1 2] and v2 =[2 3]. suppose that x =[a b], and the coordinates of x with respect of b are given by [x]b = [3 1]. calculate a. answer:. Given the basis b= {v1= [21],v2= [−11]} of r2 with associated x′y′ coordinate system shown in the figure below. in the following questions [x] is [x]b= [x]x′y, the coordinate vector of x relative to the basis b, which also is the x′y′ coordinate vector of x. find a matching answer from the given choices for each of the following. Find a formula for t (x1, x2), and use that formula to find t (2, − 3). give exact answers in the form of a fraction. 2. consider the basis s = {v1, v2, v3} for r3, where v1 = (1, 1, 1), v2 = (1, 1, 0), and v3 = (1, 0, 0), and let t:r3 → r3 be the linear operator for which t (v1) = (3, − 1, 6), t (v2) = (4, 0, 1), t (v3) = (− 1, 7, 1).
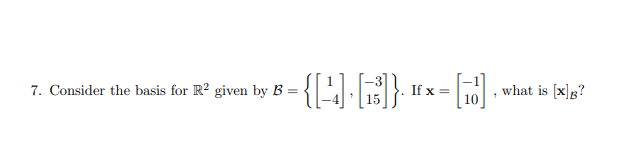
Solved 7 Consider The Basis For R2 Given By Chegg Let v1 = (1, 4, 5), v2 = (2, 3, 1), and v3 = ( 4, 1, 7) (write as column vectors). why does b = {v1, v2, v3} form a basis for ℝ^3? we need to show that b is a linearly independent set of. Let the basis b = {v1,v2} be a basis of r2, where v1 =[1 2] and v2 =[2 3]. suppose that x =[a b], and the coordinates of x with respect of b are given by [x]b = [3 1]. calculate a. answer:. Given the basis b= {v1= [21],v2= [−11]} of r2 with associated x′y′ coordinate system shown in the figure below. in the following questions [x] is [x]b= [x]x′y, the coordinate vector of x relative to the basis b, which also is the x′y′ coordinate vector of x. find a matching answer from the given choices for each of the following. Find a formula for t (x1, x2), and use that formula to find t (2, − 3). give exact answers in the form of a fraction. 2. consider the basis s = {v1, v2, v3} for r3, where v1 = (1, 1, 1), v2 = (1, 1, 0), and v3 = (1, 0, 0), and let t:r3 → r3 be the linear operator for which t (v1) = (3, − 1, 6), t (v2) = (4, 0, 1), t (v3) = (− 1, 7, 1).
