
Solved 1 Let A Bв Z Prove That If Ab2 Is Even Then A Is Chegg There are 2 steps to solve this one. not the question you’re looking for? post any question and get expert help quickly. This problem has been solved! you'll get a detailed solution from a subject matter expert that helps you learn core concepts. see answer.

Solved La Prove The Following Statement If A Be Z And Ab2 Chegg To prove that if ab is odd, then a2 b2 is even, we can use the properties of odd and even numbers. if ab is odd, both a and b must be odd, because the product of an even number with any other number (even or odd) is always even. an odd number can be expressed in the form 2k 1, where k is an integer. since a and b are odd, we can write a = 2m 1. Proof. by contrapositive, it is sufficient to prove that: for every x,y∈z, if 7 x or 7 y, then 7 xy. case 1: let 7 x, then x=7k for some k∈z. hence, xy=(7k)y=7(ky) 1. since ky∈z (by fact 3), then 7 xy. case 2: if 7 y, then 7 xy. lhs =rhs xy difference of integers are integers.(the proof is similar to case 1 and can be omitted). Proposition: for every a;b 2z, ab is even if and only if a is even or b is even. proof: let a and b be integers. first, suppose a is even or b is even. wlog, let a be even, so a = 2x for some x 2z. then ab = 2(xb), so ab is even. we conclude that, if a or b is even, then ab is even. second, suppose that both a and b are odd. Suppose $a,b,c\in\mathbb{z}$. prove by contradiction that if $a^{2} b^{2}=c^{2}$, then $a$ or $b$ is even. my proof was the following: for the sake of contradiction, suppose it is not the case that $a$ or $b$ are even. by de morgan's law, that means that $a$ and $b$ are odd.
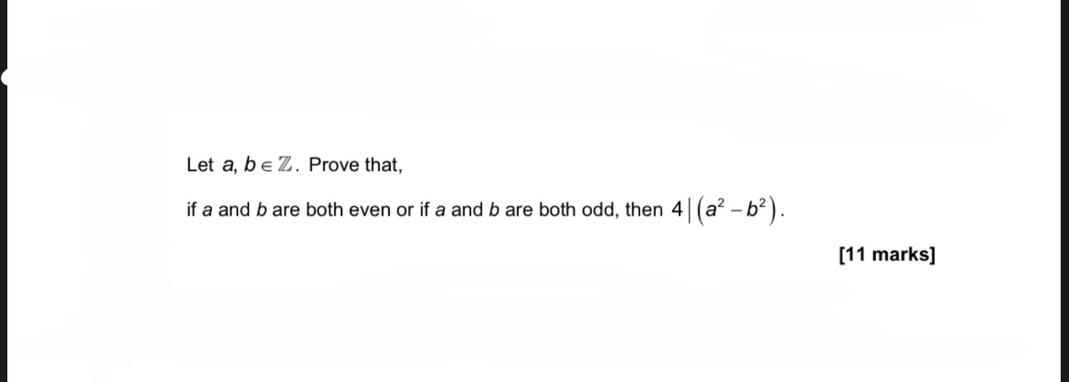
Solved Let A Bв Z Prove That If A And B Are Both Even Or If Chegg Proposition: for every a;b 2z, ab is even if and only if a is even or b is even. proof: let a and b be integers. first, suppose a is even or b is even. wlog, let a be even, so a = 2x for some x 2z. then ab = 2(xb), so ab is even. we conclude that, if a or b is even, then ab is even. second, suppose that both a and b are odd. Suppose $a,b,c\in\mathbb{z}$. prove by contradiction that if $a^{2} b^{2}=c^{2}$, then $a$ or $b$ is even. my proof was the following: for the sake of contradiction, suppose it is not the case that $a$ or $b$ are even. by de morgan's law, that means that $a$ and $b$ are odd. Find step by step discrete maths solutions and the answer to the textbook question let $a, b \in z .$ a) prove that if a2|b2 then a|b. b) is it true that if a2|b3 then a2|b3?. Prove the statement: for all integers \(a\text{,}\) \(b\text{,}\) and \(c\text{,}\) if \(a^2 b^2 = c^2\text{,}\) then \(a\) or \(b\) is even. hint . a proof by contradiction would be reasonable here, because then you get to assume that both \(a\) and \(b\) are odd. Prove or disprove that where $a, b \in z$, the number a b is even if and only if a b is even. If (a | b) and (a | c), then a | (b c), suppose a and be are integers. if (a | b), and (b | a), then a = b or a = b. and more. study with quizlet and memorize flashcards containing terms like let a, b, and c be integers.

Solved Let A Bв Z Prove That If A And B Are Both Even Or If Chegg Find step by step discrete maths solutions and the answer to the textbook question let $a, b \in z .$ a) prove that if a2|b2 then a|b. b) is it true that if a2|b3 then a2|b3?. Prove the statement: for all integers \(a\text{,}\) \(b\text{,}\) and \(c\text{,}\) if \(a^2 b^2 = c^2\text{,}\) then \(a\) or \(b\) is even. hint . a proof by contradiction would be reasonable here, because then you get to assume that both \(a\) and \(b\) are odd. Prove or disprove that where $a, b \in z$, the number a b is even if and only if a b is even. If (a | b) and (a | c), then a | (b c), suppose a and be are integers. if (a | b), and (b | a), then a = b or a = b. and more. study with quizlet and memorize flashcards containing terms like let a, b, and c be integers.
