Solved 1 Show That The Problem Max C1x1 C2x2 S T X1 Chegg

Solved Consider The Following Problem Max Z X1 A Solve Chegg Our expert help has broken down your problem into an easy to learn solution you can count on. Question asked by ramenle consider problem max c1x1 c2x2 s.t. x 1 <= 10 ax 1 bx 2 <= d x 1,x 2 >= 0 suppose c 1 = 8, c 2 = 14, d = 3 give values for a, b such that the problem : (a) has a unique solution. (b) has no feasible solutions. (d) is unbounded.

Solved Maxc1 C2 Smax Subject To U Min C1 C2 C1 S W Budget Chegg Homework 5(partial solutions) let c = b[x0; r], where x0 2 rn and r > 0 are given. find you can easily derive this formula from the projection onto b[0; r] using an a ne change of coordinates. problem 10.6 consider the maximization problem max x2. Consider the problem maximize s.t. c1x1 c2x2 x1 x2 ≤ 1. x1,x2 ≥ 0 where c1 and c2 are constants such that c1>c2 ≥ 0. this is a linear programming problem. assuming that the problem has an optimal feasible solution, use the fonc to show that the unique optimal feasible solution x∗ is (1,0)t. How to solve the linear programming maximization problem that contains both <= and >= equations? for example here's a case: maximize: subject to: where a1, a2, a3, a4, a5, a6, b1, b2, b3, c1, c2, c3 are the constants in the given equations. what will be the proper matlab code to solve this problem? z = [c1 ; c2 ; c3]; a = [ a1 a2 a3 ; . To find such values for a and b, we need to solve the system of equations: 10a 0b = d a, b >= 0 b <= a 10 since d = 3, we have: 10a = 3 a = 3 10 b <= 3 100 therefore, one possible solution for a and b that gives an unbounded solution is a = 3 10 and b = 1 30.
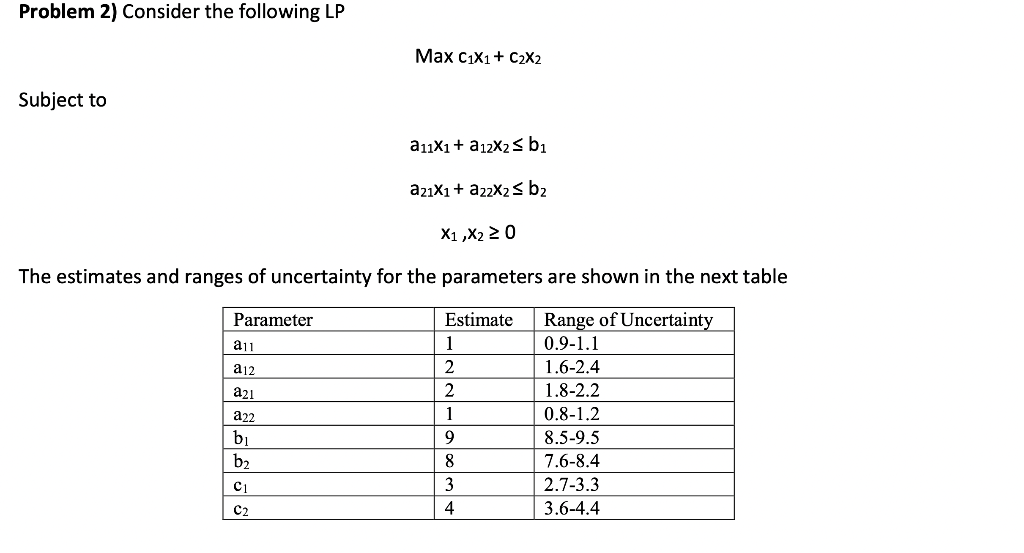
Problem 2 Consider The Following Lp Maxc1x1 C2x2 Chegg How to solve the linear programming maximization problem that contains both <= and >= equations? for example here's a case: maximize: subject to: where a1, a2, a3, a4, a5, a6, b1, b2, b3, c1, c2, c3 are the constants in the given equations. what will be the proper matlab code to solve this problem? z = [c1 ; c2 ; c3]; a = [ a1 a2 a3 ; . To find such values for a and b, we need to solve the system of equations: 10a 0b = d a, b >= 0 b <= a 10 since d = 3, we have: 10a = 3 a = 3 10 b <= 3 100 therefore, one possible solution for a and b that gives an unbounded solution is a = 3 10 and b = 1 30. Overall, the problem was converted to canonical form by introducing slack and surplus variables and expressing the constraints as a system of linear equations. the optimal solution can be found by graphically analyzing the feasible region and calculating the objective function for each corner point. Consider the following linear program max c1x1 c2x2, subject to 12x1 3x2 ≤ 60, 3x1 − x2 ≥ −7, x2 ≤ 10, x1 ≥0,x2 free. homework #3 (a) for an lp with m main constraints and n variables. To determine the correct answer, we need to analyze the given optimal solution (1,0,3) and the constraints of the linear programming problem. optimal solution: the optimal solution (1,0,3) means that x1 = 1, x2 = 0, and x3 = 3. this solution satisfies all the constraints: x1 x2 x3 = 1 0 3 = 4 ≤ 4 x1 = 1 ≤ 2. Video answer: we are given with the objective function, maximum of z to be equal to x, 1 plus 3 x 2, and we are also given with the subject to constraint, x, 1 plus x, 2, less than or equal to 2 and minus x, 1.

Solved 1 Consumption Problem Max U C1 C2 C1 C2 St P1c1 Chegg Overall, the problem was converted to canonical form by introducing slack and surplus variables and expressing the constraints as a system of linear equations. the optimal solution can be found by graphically analyzing the feasible region and calculating the objective function for each corner point. Consider the following linear program max c1x1 c2x2, subject to 12x1 3x2 ≤ 60, 3x1 − x2 ≥ −7, x2 ≤ 10, x1 ≥0,x2 free. homework #3 (a) for an lp with m main constraints and n variables. To determine the correct answer, we need to analyze the given optimal solution (1,0,3) and the constraints of the linear programming problem. optimal solution: the optimal solution (1,0,3) means that x1 = 1, x2 = 0, and x3 = 3. this solution satisfies all the constraints: x1 x2 x3 = 1 0 3 = 4 ≤ 4 x1 = 1 ≤ 2. Video answer: we are given with the objective function, maximum of z to be equal to x, 1 plus 3 x 2, and we are also given with the subject to constraint, x, 1 plus x, 2, less than or equal to 2 and minus x, 1.
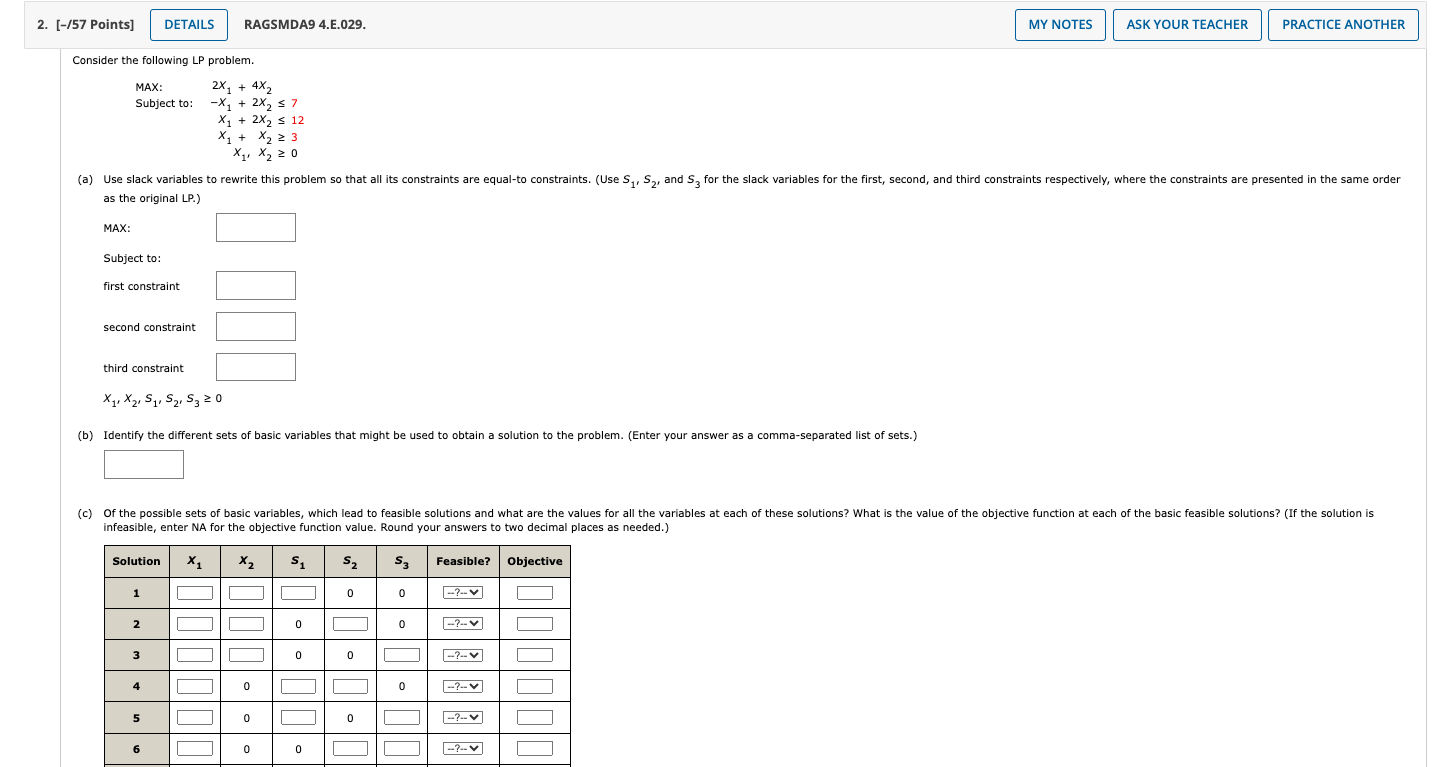
Solved Consider The Following Lp Problem Max 2x1 4x2 Chegg To determine the correct answer, we need to analyze the given optimal solution (1,0,3) and the constraints of the linear programming problem. optimal solution: the optimal solution (1,0,3) means that x1 = 1, x2 = 0, and x3 = 3. this solution satisfies all the constraints: x1 x2 x3 = 1 0 3 = 4 ≤ 4 x1 = 1 ≤ 2. Video answer: we are given with the objective function, maximum of z to be equal to x, 1 plus 3 x 2, and we are also given with the subject to constraint, x, 1 plus x, 2, less than or equal to 2 and minus x, 1.
Comments are closed.