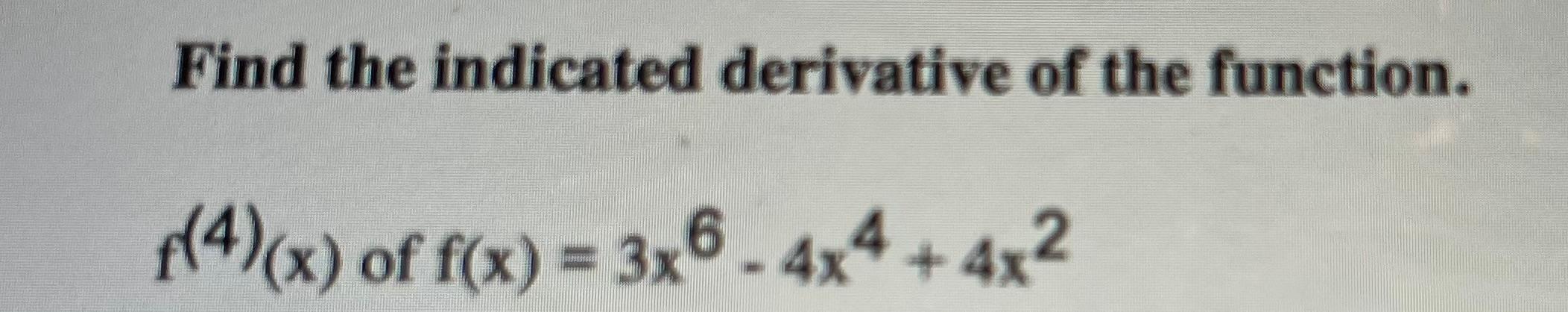
Solved Sketch The Derivative Of The Graph Find The Indicated Chegg Sketch the derivative f' (x) for each of the graphs of f (x) given below. you may use a different color on the same graph or graph the derivative on a graph below the function. How to "go backwards" given the graph of a derivative f'(x), how to sketch the graph of the function f(x) no equations given! 3 examples shown: easy (li.

Select The Correct Sketch Of The Derivative Of The Chegg Exercise 1. sketch the derivatives of graphs 1 and 2. exercise 3. sketch the derivatives of graphs 3 and 4. exercise 4. what is an important difference between the derivative of graph 3 and the derivative of graph 4? use terminology from calculus. the derivative of graph 4 is not continuous. exercise 5. sketch the derivatives of graphs 5 and 6. Solution as the graph of f'(x) is a straight line with equation y = c (degree = i), will be a quadratic function (degree = 2). the turning point at x = o. {x: x < o}: gradient is negative (as the graph is iccated telow the x axis) and in magnitude. {x: x o}: gradient is pcsitive and is increasing in magnitude. 24. let 𝑓 be a function that is continuous on the closed interval >0,4 ?. the function 𝑓 and its derivatives have the properties indicated in the table below. (a) find the 𝑥 coordinate of each point at which 𝑓 attains a maximum value or a minimum value. (b) find the 𝑥 coordinate of each point of inflection on the graph of 𝑓. Sketch the derivative f'(x) for each of the graphs of f(x) given below. you may use a different color on the same graph or graph the derivative on a graph below the function. state the points where the function is not differentiable and explain why not. y=f(x) vf 10 y=f(x) em m 3 10.
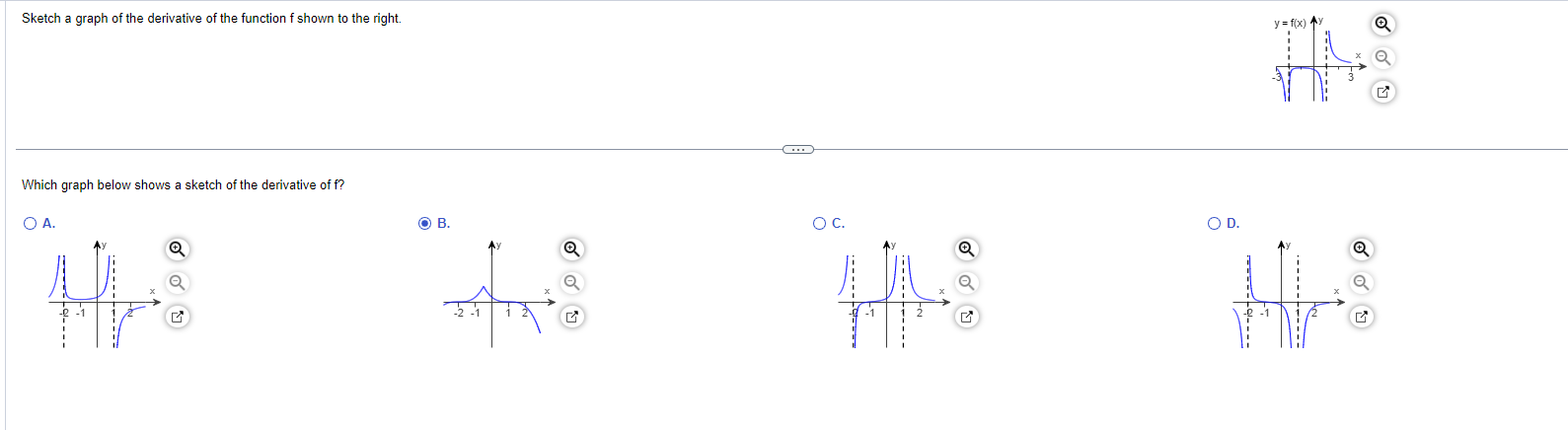
Solved Sketch A Graph Of The Derivative Of The Function F Chegg 24. let 𝑓 be a function that is continuous on the closed interval >0,4 ?. the function 𝑓 and its derivatives have the properties indicated in the table below. (a) find the 𝑥 coordinate of each point at which 𝑓 attains a maximum value or a minimum value. (b) find the 𝑥 coordinate of each point of inflection on the graph of 𝑓. Sketch the derivative f'(x) for each of the graphs of f(x) given below. you may use a different color on the same graph or graph the derivative on a graph below the function. state the points where the function is not differentiable and explain why not. y=f(x) vf 10 y=f(x) em m 3 10. For each of the following graphs of the function y = f (x), make a rough sketch of the derivative function f' (x). by comparing the graphs of f (x) and f' (x), show that the intervals for which f (x) is increasing correspond to the intervals where f' (x) is positive. F0(x) = lim h!0 f(x h) f(x) h: if this limit exists, then f0(x) is the slope of the tangent line to the graph of f at the point (x;f(x)). consider the graph of f(x) below: 1.use the graph to answer the following questions. (a)are there any values x for which the derivative f0(x) does not exist? (b)are there any values x for which f0(x) = 0?. Given the graph of f(x), sketch an approximate graph of f '(x). 1) x f(x) a) x f '(x) b) x f '(x) c) x f '(x) *d) x f '(x) 2) x f(x) a) x f '(x) *b) x f '(x) c) x f '(x) d) x f '(x). Using the graph of f(x) = x3 — 6x2 ox, sketch the graph of f'(x) and f" (x) on the same axes. solution to sketch f'(x), begin by identifying the position of the local maximum and local minimum. through these points, draw vertical lines to separate the intervals where the slope of the tangent line is positive from.
